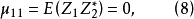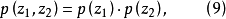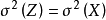復隨機變數

設X，Y是定義在同一個慨率空間上的兩個實隨機變數，稱Z=X+iY為一個復隨機變數，其中i²=-1。復隨機變數X+iY本質上是二維隨機變數(X，Y)，具有二維隨機變數的一些性質。例如，實二維隨機變數(X₁，Y₁)，(X₂，Y₂)，…，(X_n，Y_n)相互獨立，那么復隨機變數X₁+iY₁，X₂+iY₂，…，X_n+iY_n也相互獨立。當復隨機變數Z=X+iY的實部X與虛部Y都有有限的數學期望，就定義E[Z]=E[X]+iE[Y]為Z的數學期望，若E[X]、E[Y]至少有一個不存在，就說E[Z]不存在。關於隨機變數數學期望的一些性質，對復隨機變數也成立。

基本介紹

• 中文名：復隨機變數
• 外文名：complex random variable  
• 所屬學科：數學（統計學）
• 相關概念：複數，隨機變數，數學期望等

基本介紹

一些重要的量往往是複數，如周期信號的傅立葉係數就是複數，因此需要一種記號，以便於處理取值為複數的隨機變數 ，即

式中：實部X和虛部Y都是實隨機變數。

復隨機變數的密度函式

復隨機變數Z的實部X和虛部Y的聯合機率密度，稱為復隨機變數Z的密度函式，即

式中： 為一個實數。

期望值、方差和協方差

若將實隨機變數的期望值、方差和協方差推廣至復隨機變數時，則要求：

(1)當實隨機變數Y=0(或X=0)時，復隨機變數Z的矩應當等於實隨機變數X(或Y)的矩。

(2)必須保持隨機變數的矩的特性(如方差應為非負實數)。

期望值

復隨機變數Z的期望值規定為

當Y=0時， ，符合前述要求。

方差

復隨機變數Z的方差規定為

式中：上標*表示共軛。若Y=0，則 ，符合要求。

協方差

兩個復隨機變數 和 之間的協方差規定為

如果 ，則有 ，符合要求。

對於隨機復向量X和Y，可推廣上述定義。其中，協方差矩陣表示成

式中：上標H表示取共軛轉置。

復隨機變數的相關性

若復隨機變數 和 的協方差為零，即

則稱復變數和不相關。

若復隨機變數和的二階混合矩為零，即

則稱復變數和正交。

若復隨機變數和的密度函式滿足

則稱復變數和獨立。