傅立葉係數由Fourier coefficient 翻譯而來,有多箇中文譯名。它是數學分析中的一個概念,常常被套用在信號處理領域中。對於任意的周期信號,如果滿足一定條件,都可以展開三角函式的線性組合,每個展開項的係數稱為傅立葉係數。
基本介紹
- 中文名:傅立葉係數
- 外文名:Fourier coefficient
- 別稱:傅立葉係數
- 歸屬學科:數學
- 基本釋義:信號的傅立葉級數的係數
- 套用:信號處理
數學分析
定義



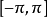






一般的周期函式






偶函式






奇函式






相關定理

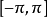





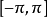



信號與系統
三角傅立葉級數







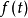













指數傅立葉級數



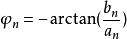

傅立葉係數由Fourier coefficient 翻譯而來,有多箇中文譯名。它是數學分析中的一個概念,常常被套用在信號處理領域中。對於任意的周期信號,如果滿足一定條件,都可以展開三角函式的線性組合,每個展開項的係數稱為傅立葉係數。











































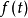
















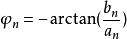
傅立葉係數由Fourier coefficient 翻譯而來,有多箇中文譯名。它是數學分析中的一個概念,常常被套用在信號處理領域中。對於任意的周期信號,如果滿足一定條件,都可以...
在單變元情形,常把傅立葉級數σ(f)寫成實形式,其中的ak稱為f的餘弦傅立葉係數。...... ,常把傅立葉級數σ(f)寫成實形式,其中的ak稱為f的餘弦傅立葉系...
傅立葉展開式(Fourier expansion)是指用三角級數表示的形式,即一個函式的傅立葉級數在它收斂於此函式本身時的一種稱呼。若函式f(x)的傅立葉級數處處收斂於f (...
* 傅立葉變換的逆變換容易求出,而且形式與正變換非常類似; * 正弦基函式是微分運算的本徵函式,從而使得線性微分方程的求解可以轉化為常係數的代數方程的求解.線上...
熱傳導定律也稱為傅立葉定律,表明單位時間內通過給定截面的熱量,正比例於垂直於...比例常數κ是一個輸運特性,稱為熱導率(也稱為 導熱係數),單位是 (W·m-1...
傅立葉數(英語:Fourier number;Fo)在物理學及工程學領域是一個用來描述非穩態熱傳導及分子擴散的無因次量。以約瑟夫·傅立葉之名命名。概念上,它的物理意義是...
傅立葉分析Fourier analysis 分析學中18世紀逐漸形成的一個重要分支,主要研究函式的傅立葉變換及其性質。又稱調和分析。在經歷了近2個世紀的發展之後,研究領域已從...
傅立葉級數是一類特殊的三角級數。當n≥2時,常稱σ(f)為多重傅立葉級數。...... 為f的傅立葉係數,這裡m=(m1,m2,...,mn)是n元整點,其全體記為Zn,m...
傅立葉-比當定理(Fourier-Budan theorem)是關於實係數多項式在確定區間內根的個數的一個命題,該定理斷言:設f(x)是一個實係數n次多項式,如果f(a)≠0,f(b)≠...
特點 具有三維周期性的晶體結構對應的晶體電子密度函式p ( .r,,,:)可用止交、歸一的正弦、餘弦函式組或正交、歸一的指數函式組進行傅立葉級數展開,當選擇指數...
傅立葉反演公式是經典傅立葉公式的推廣。在數學中,傅立葉反演定理說,對於許多類型的函式,可以從其傅立葉變換中得到原函式。 直觀地,它可以被視為,如果我們知道...
《漫畫傅立葉解析》是2009年8月1日科學出版社出版的圖書,作者是涉谷道雄,漫畫繪製是HaruseHiroki,漫畫編制是株式會社TRENO-PRO,翻譯是陳芳。...
廣義傅立葉級數(generalized Fourier series)是特殊的正交級數,函式f(r)在區間[0,a]上具有二階連續導數,則f(r)可以展開成以貝塞爾函式為基的廣義傅立葉級數。...
讓·巴普蒂斯·約瑟夫·傅立葉(Baron Jean Baptiste Joseph Fourier,1768年3月21日-1830年5月16日),法國歐塞爾人,著名數學家、物理學家。1780年,就讀於地方軍校...
傅立葉變換紅外光譜儀(Fourier Transform Infrared Spectrometer,簡寫為FTIR Spectrometer),簡稱為傅立葉紅外光譜儀。它不同於色散型紅外分光的原理,是基於對干涉後的...
占空係數是由導線的截面積、匝數、層數、絕緣厚度及繞組的匝間距離等決定,是指...脈寬調製波形同時應能明顯看出從一個周期到另一個周期,傅立葉分量的幅值將隨著...
對上面獲得的結果進行離散傅立葉反變換,變換到倒頻譜域。 MFCC就是這個倒頻譜圖的幅度(amplitudes)。一般使用12個係數,與訊框能量疊加得13維的係數。 [1] 梅爾...
的傅立葉係數是 [1] 於是 的傅立葉級數只含有餘弦函式的項,即其中 如(3)所示。(4)式右邊的級數稱為餘弦級數。當 ,則偶函式 所展開成的餘弦函式為其中...
里斯-費希爾定理是貝塞爾不等式的逆命題。貝塞爾不等式表明:{ck}為L2[a,b]中某個函式的傅立葉係數的必要條件是{ck}2的和函式收斂,里斯-費希爾定理表明這個條件...
周期信號的帕賽瓦爾定理就是說 周期信號可以等效為各次諧波的疊加,因此傅立葉係數的平方求和 (也就是各次諧波的功率和)與原信號的功率是相等的;...
Fourier分析,即傅立葉分析,是數學的一個分支領域。它研究如何將一個函式或者信號表達為基本波形的疊加。它研究並擴展傅立葉級數和傅立葉變換的概念。基本波形稱為...
在數學分析中,以Marc-Antoine Parseval命名的帕塞瓦爾恆等式是一個有關函式的傅立葉級數的可加性的基礎結論。表示可積函式與其傅立葉係數之間關係的恆等式。從幾何...
的復傅立葉係數。這些積分不隨輪廓 的變形而改變是斯托克斯定理的直接結果。在實踐中,上述的積分公式可能不是計算給定的函式 係數 最實用的方法;相反,人們常常通過...
TP(a)}o一P (a卯=f稱為特普利茨方程.當a(t)}0時,此類方程也滿足諾特定理,其指標}c= Ind a (t).設a(t>有傅立葉係數{(a;} (}=o,士1,...},...
