水文隨機變數

水文隨機變數（hydrologic random variable）受隨機因素影響，遵循統計規律變化的水文變數。

基本介紹

• 中文名：水文隨機變數
• 外文名：hydrologic random variable
• 釋義：遵循統計規律變化的水文變數
• 形式：以分布函式來反映其統計規律性

簡介

水文隨機變數在未來任一時刻出現的數值無法準確預測，但能以分布函式(或等價的機率密度函式)來反映其統計規律性，也

就是表示其各種數值出現的可能性。分布函式的形式，可根據水文隨機變數資料按水文統計學的有關原理和方法予以確定。

水文隨機變數

其他

分布函式與機率密度函式

式中x為隨機變數；F（xp；）為分布函式;f(t;θ)為機率密度函式;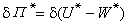

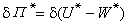水文隨機變數

為x大於或等於xp這一事件出現的機率;xp稱為x的p分位數,或超過機率為p的設計值。上式常以圖形的方式表示,稱為頻率曲線(見圖)。

水文隨機變數

主要目的

確定水文隨機變數的分布函式及其所含的參數，是研究水文隨機變數的主要目的。水文學中常用的分布函式有以下幾種：皮爾遜Ⅲ型分布、對數皮爾遜Ⅲ型分布、對數常態分配、 概化極值分布、 韋克貝分布、克里茨基－門克爾分布等。在中國主要使用皮爾遜Ⅲ型分布。其機率密度函式如下：

x≥α　γ〉0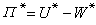

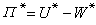水文隨機變數

式中α、β、γ為待估參數;Γ(γ)為伽瑪函式。三個參數α、β、γ與隨機變數x的三個主要數字特徵值（數學期望Ex、方差σ婌、偏態係數Cs）有一定的關係，可相互推求。這種情況對其他分布也是如此。不過不同的分布,參數與特徵值之間的關係不同而已。在參數估計時，有的方法，如極大似然法，是先估計參數α、β、γ，然後由有關公式可求得相應的Ex、Cv（離勢係數）與Cs；有的方法，如矩法或適線法，是先估計出Ex、Cv及Cs，需要時，可由有關公式求出相應的參數值。

形式

，除用上述假設檢驗的方法外（見水文統計學），還使用導出分布的方法，即考慮水文變數的物理性質並做若干假定，再經推導而得。其中又可分為依據事件的模型和聯合機率的模型。由於問題複雜，為便於推導而作的假定常與實際情形相差較遠，故此種途徑尚處於研究階段，有時可在缺乏資料的小流域上套用。

水文學