如果複數是一個變數,則稱為復變數。一個復變數s有一個實部α、一個虛部ω,即s=α+jω。它可以用s複平面上的一個點來表示。
基本介紹
- 中文名:復變數
- 外文名:complex variable
- 所屬學科:數理科學
- 表達式:s=α+jω
- 相關概念:複數、複平面、複變函數等
定義

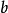

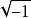
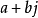
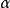
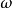

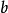

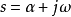
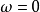
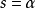
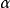
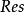
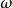
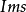
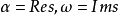
表示方法
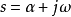
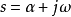
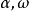
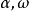
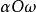
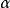

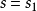
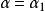
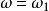
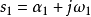
 圖1 坐標表示法
圖1 坐標表示法 圖2 向量表示法
圖2 向量表示法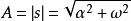

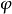
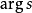
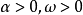
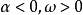
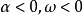
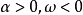
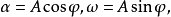
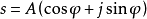
乘積定理
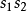
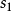
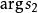
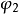
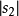
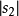
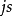

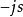


商定理

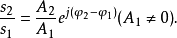

如果複數是一個變數,則稱為復變數。一個復變數s有一個實部α、一個虛部ω,即s=α+jω。它可以用s複平面上的一個點來表示。

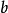

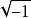
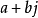
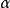
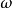

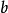

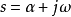
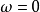
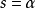
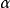
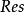
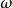
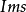
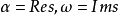
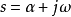
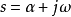
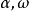
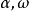
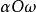
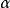

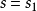
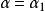
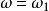
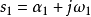
 圖1 坐標表示法
圖1 坐標表示法 圖2 向量表示法
圖2 向量表示法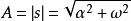

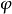
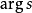
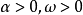
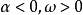
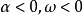
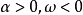
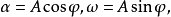
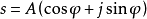
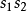
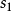
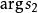
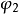
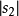
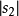
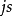

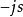



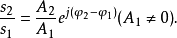
《復變數(第2版)》是Cambridge《套用數學系列叢書》之一,內容相當精闢,巧妙地展示了復變數在數學科學中的核心地位以及其在工程和物理科學套用中的關鍵性作用。復...
如果複數是一個變數,則稱為復變數。一個復變數s有一個實部α、一個虛部ω,即s=α+jω。它可以用s複平面上的一個點來表示。...
復變指數函式是實變數指數函式在複數域中的推廣。形如ez=ex+iy=ex(cos y+isin y)的函式稱為復變指數函式。...
復變對數函式是實變數對數函式在複數域中的推廣。若ew=z(z≠0,∞),則複數w稱為複數z的對數,記為w=Logz=log|z|+i(arg z+2kπ)(k=0,±1,±2,......
復變三角函式是實變數三角函式在複數域中的推廣。當z為實數時,復變三角函式定義與數學分析中關於正弦函式和餘弦函式的定義是一致的。...
復變根式函式是實變數根式函式在複數域中的推廣。...... 復變根式函式是實變數根式函式在複數域中的推廣。形如, 的函式稱為復變根式函式,其中n是大於1的正整數...
《復分析導論:多復變函式》是2008年高等教育出版社出版的圖書,作者是沙巴特。本書主要介紹了多變數全純函式、基本的幾何概念、解析延拓、亞純函式和留數等知識。...
復變反三角函式是實變數反三角函式在複數域中的推廣,由此定義復變反正弦函式,同樣地可定義復變反餘弦函式和復變反正切函式。...
復變一般指數函式是實變數一般指數函式在複數域中的推廣。若a≠0,∞,則稱函式w=az=ezlog a為復變一般指數函式。...
復變冪函式是實變數冪函式在複數域中的推廣。形如w=za=ealnz(z≠0,∞,a為復常數)的函式稱為復變冪函式。...
《復變函式與積分變換》是2014年8月8日清華大學出版社出版的圖書,作者是河北科技大學理學院數學系。...
初等復變eT}數(elementary functions of a com- plex variable)實變數初等函式在複數域中的推廣。...
到 1850 年俄國數學家切比雪夫首開記錄,證明了1896 年法國的阿達瑪和比利時數學家瓦萊.普桑分別用高深的復變數的整函式理論和黎曼的 zeta 函式證明了這個定理,但...
為簡化計算而建立的實變數函式和復變數函式間的一種函式變換。對一個實變數函式作拉普拉斯變換,並在複數域中作各種運算,再將運算結果作拉普拉斯反變換來求得實數域...
何為多複分析?已故著名數學家鐘家慶先生在為《中國大百科全書》數學卷撰寫多複變函數論條目時,稱多複變函數論是"數學中研究多個復變數的全純函式的性質和結構的...
4、傳遞函式是單變數系統描述,外部描述。5、傳遞函式是在零初始條件下定義的,不能反映在非零初始條件下系統的運動情況。6、一般為復變數 S 的有理分式,即 n ...
雙側拉普拉斯變換(bilateral Laplace transformation)是一種積分變換,作用對象是任意實數t的實數函式或是復變函式 f(t),作用結果是F(s),其形式類似機率中的動差...
與自守函式的工作不同,龐加菜在整函式和多復變數函式方面作出的貢獻打開了新研究領域的大門.相關領域的研究成果豐富.並一直持續到如今[2] 。...
s, 是一個復變數;mathcal 是一個運算符號,它代表對其對象進行拉普拉斯積分int_0^infty e^ ,dt;F(s),是f(t),的拉普拉斯變換結果。...
在複分析中,最大模原理說明如果單變數復變函式 f 是一個全純函式,那么它的模|f| 的局部最大值不可能在其定義域的內部取到。...
是有算術有意義和算術背景的L-函式· 例如黎曼在研究高斯和勒讓德提出的素數定理時,引出了和素數分布有關的復變數的黎曼zeta-函式。...
有理正實函式(rational positive real function)一類復變數有理函式...... 有理正實函式(rational positive real function)一類復變數有理函式.有理正實函式(rationa...
常微分方程解析理論是在複數域上研究微分方程解的性質的數學分支,19世紀中葉,柯西(Cauchy,A,-L)證明了在相當廣泛的條件下微分方程的解是復變數的解析函式,由此...
