弗羅貝尼烏斯定理(經典形式)(Frobenius the-orem (classical form ))弗羅貝尼烏斯定理在R中的形式。
基本介紹
- 中文名:弗羅貝尼烏斯定理(經典形式)
- 外文名:Frobenius the-orem (classical form )
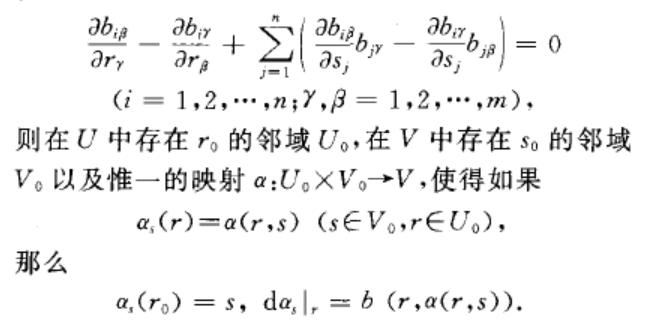
弗羅貝尼烏斯定理(經典形式)(Frobenius the-orem (classical form ))弗羅貝尼烏斯定理在R中的形式。
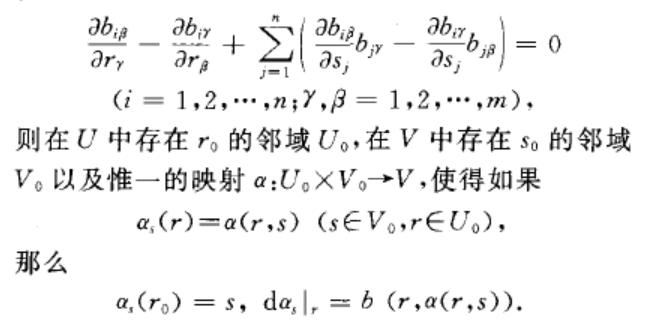
弗羅貝尼烏斯定理(經典形式)(Frobenius the-orem (classical form ))弗羅貝尼烏斯定理在R中的形式。弗羅貝尼烏斯定理(經典形式)(Frobenius the-orem (classica...
經典形式 弗羅貝尼烏斯定理(經典形式)是弗羅貝尼烏斯定理在Rⁿ中的形式。設U與V分別是R與Rⁿ中的開集,R中坐標用r₁,r₂,...,rₘ表示,Rⁿ中坐標用s₁,s₂,...,sₙ表示。令b:U×V→A(n,m)為U×V到所有n×m實矩陣的集合的一個C映射。設(r₀,s₀)∈U×V,若在U×V上 則...
弗羅貝尼烏斯問題(Frobenius problem)是關於一次不定方程的一個著名問題。設a₁,a₂,…,aₙ為整數,它們的最大公約數為1,求不能表示成a₁x₁+a₂x₂+…+aₙxₙ的最大整數,其中x₁,x₂,…,xₙ為任意非負整數。這個問題稱為一次不定方程的弗羅貝尼烏斯(Frobenius)問題,也稱為...
弗羅貝尼烏斯定理(第一形式)弗羅貝尼烏斯定理(第一形式)是一個數學術語。弗羅貝尼烏斯定理(第一形式)<Frobenius the-orem (first form)積分流形存在性定理.該定理斷言:若少是微分流形M上的一個。維光滑的對合分布,pEM,則存在通過p的少的一個積分流形.
算術-幾何平均不等式(inequality of arithmeticand geometric mean)著名經典不等式之一設ai,az}...}a,,均為正數,則它們的算術平均值不小於它們的幾何平均值,即一條線段既分成相等的(兩條)線段,再分成不相等的(兩條)線段,則由二不相等的線段構成的矩形與兩個分點之間一段上的正方形的和等於原來線段一半上...
弗羅貝尼烏斯不等式的證明 弗羅貝紐斯(Frobenius)不等式 設A、B、C分別為m×n,n×s,s×t矩陣,則:r(ABC)≥r(AB)+r(BC)-r(B)。證明: 只要證明:即可。事實上,因為 所以 即 下面西爾維斯特(Sylvester)不等式也可由弗羅貝紐斯不等式的直接推得。故有的書籍也將其稱為弗羅貝紐斯不等式。西爾維斯特...
關於這一類群有一個著名的弗羅貝尼烏斯定理:若G是Ω上的一個弗羅貝尼烏斯群,則G中全部在Ω上沒有不動點的元素,連同G的單位元素組成G的一個正則的正規子群.這個定理早在1902年就由弗羅貝尼烏斯(Frobenius,F.G.)證明了,但不論是弗羅貝尼烏斯的原始證明,還是以後改進了的證明,都需要使用群特徵標理論,人們...
第二形式)弗羅貝尼烏斯定理(第二形式)是一個數學術語。弗羅貝尼烏斯定理(第二形式)(Frobenius theorem (second form))理想的積分流形存在性定理.設CO(M)是由n-m個獨立的局部生成的〕形式微分理想,n=dim(M) (m<n).設pEM,則有在惟一的通過p的中的最大連通積分流形,且這個積分流形的維數為m.
弗羅貝尼烏斯方法(Frobenius method)是尋求n階方程在正則奇點鄰域的解的一種方法。簡介 弗羅貝尼烏斯方法是尋求n階方程在正則奇點鄰域的解的一種方法。實例 以二階方程為例來說明這個方法,即討論 依正則奇點假設,取 ,而 (1)即化為 弗羅貝尼烏斯建議取形式解 使對(1)要求滿足 其中 ,設α,β為 p(λ)...
定理1 對每個素數p和任一正整數n,存在一個唯一的 個元素的有限域,它就是 在 上的分裂域,除此之外無其它 個元素的有限域。 個元素的有限域習慣記成 或 , 。最後指出有限域 有一個很重要的自同構即弗羅貝尼烏斯(Frobenius)自同構,利用特徵p>0的域的一條性質 ,作一個 到自身的映射 ,...
弗羅貝尼烏斯互反律(Frobenius reciprocity)在特徵標計算中將誘導特徵標與限制特徵標聯繫起來的重要公式.設X是群G的兩個復特徵標,定義X與必的內積 弗羅貝尼烏斯互反律(Frobenius reciprocity)在特徵標計算中將誘導特徵標與限制特徵標聯繫起來的重要公式.設X是群G的兩個復特徵標,定義X與必的內積 ...
弗羅貝尼烏斯映射是在伽羅瓦理論中起著重要作用的映射。弗羅貝尼烏斯映射(Frobenius mapping)在伽羅瓦理論中起著重要作用的映射.對特徵為h的域F,映射7T:F~F,{二~x}'稱為弗羅貝尼烏斯映射.實際上,n是F到它的子域F"=x"{xEF}的一個域同態.對於特徵p>0的域,它是一個單一同態.若這個同態又是滿同態,也就...
弗羅貝尼烏斯代數(Frobenius algebra)擬弗羅貝尼烏斯代數的子類.設A是域F上代數,若左正則樟}A與右正則樟A}的對偶模。定義 弗羅貝尼烏斯代數(Frobenius algebra)擬弗羅貝尼烏斯代數的子類.設A是域F上代數,若左正則樟}A與右正則樟A}的對偶模 作為左A模與A同構,則稱A為弗羅貝尼烏斯代數.A是弗羅貝尼烏斯代數的...
弗羅貝尼烏斯態射(Frobenius morphism)是特徵p的概形上特有的態射。設k是一個特徵p>0的域。對任意一個k上的概形X,可以定義一個X到自身的態射F:X→X,它把每個點映到自身,而把每個(定義在開子集上的)函式映成自身的p次冪。F稱為X的絕對弗羅貝尼烏斯態射。概念 弗羅貝尼烏斯態射(Frobenius morphism)是特徵p...
弗羅貝尼烏斯準則 弗羅貝尼烏斯準則(Frobenius criterion)有關p冪零性的一個極好判別準則.該準則斷言:一個有限群為p冪零群(即p‘閉群),若且唯若它是P齊性群.
弗羅貝尼烏斯同態(Frobenius homomor -phism)弗羅貝尼烏斯同態(Frobenius homomor -phism)素特徵域上代數群的一類自同態.若基域K的特徵數p>0,則映射F: (a;;)--}(叱)是GL(n,K)到自身上的一個代數群同態(它還是抽象群的同構,但不是代數群的同構).F是弗羅貝尼烏斯同態最簡單的例子一般地,設G是簡約...
弗羅貝尼烏斯補(Frobenius complement)是傳遞置換群的特殊子群(參見“弗羅貝尼烏斯群”).若H是有限群G的一個弗羅貝尼烏斯補,則G=HN,H(}N=1,且NQG,其中N為G的弗羅貝尼烏斯核。區(block)集合f2由於置換群G的作用而產生的一些子集.設G是月上的傳遞置換群.若月可以表示成一些子集乙,,乙:,…,乙,的無交...
1897~1910年,他和別人證明了一系列群表示論的基本結果,如任何表示由若干不可約表示組成,誘導表示的概念等。由此不僅導出有限群的一系列重要結果(如關於表示重數的弗羅貝尼烏斯定理),而且還可以推廣到連續群的表示論上。 主要作品 弗羅貝尼烏斯的主要論文收集在《弗羅貝尼烏斯全集》(3卷,1968)中。
陳氏定理 採樣定理 抽屜原理 D 德·摩根定律 迪尼定理 等周定理 代數基本定理 多項式餘數定理 大數定律 狄利克雷定理 棣美弗定理 棣莫弗—拉普拉斯定理 笛卡爾定理 多項式定理 笛沙格定理 E 二項式定理 F 富比尼定理 范德瓦爾登定理 費馬大定理 法圖引理 費馬平方和定理 法伊特-湯普森定理 弗羅貝尼烏斯定理 費馬小...
定義 擬弗羅貝尼烏斯代數(quasi-Frobenius alge-bra)簡稱QF代數一類重要的特殊代數.域F上代數A,若它的一切投射模都是內射模,等價地說,它的正則模是內射模,則稱A為擬弗羅貝尼烏斯代數.這類代數也可從代數內部刻畫:代數A是擬弗羅貝尼烏斯代數若且唯若A的左、右理想格反同構.域F上代數A是QF代數若且唯若A是...
相關定理 定理1 (弗羅貝尼烏斯定理) 設 是定義在開子集 上的 維光滑分布,如果 滿足弗羅貝尼烏斯條件,則在每一點 ,存在局部坐標系 ,使得 ,並且 定理2 設M是具有第二可數公理的m維光滑流形,是M上的h維光滑分布,如果 滿足弗羅貝尼烏斯條件,則對於任意一點 ,必存在 的唯一的一個極大積分流形經過點p,...
性質 弗羅貝尼烏斯定理保證存在唯一的穿過V中每一點的葉,並將V分解為k維子流形L,k為可積叢F的階。相關概念 (V,F)的葉狀結構坐標卡為V的坐標系φ:,滿足對U中任意x,有 ,其中φ(x)=(y₀,y)∈ (V,F)的光滑橫截為V的子流形N,且對N中任意x,切空間TₓN橫截於Fₓ,即 。
無限群指元素個數為無限的群。拓撲群,李群,(無限)典型群,代數群,算術群,都是無限群。無限群的研究開始於19世紀下半葉。正當抽象群的概念形成之際,數學家們注意到了一類元素個數為無限的群。1879年弗羅貝尼烏斯在他的文章中開始提到抽象群,而德國數學家C.F.克萊因在他著名的“埃朗根綱領”中則使用無限...
希爾伯特基定理:若R是諾特環,則R[X] 亦然。由歸納法可知,對任意正整數n,亦然。任一個交換環R上的有限生成代數皆可表成某個 的商環。數學中的角色 多項式環對理想的商是構造環的重要技術。例子包括從同餘系 構造有限域,或從實數構造複數等等。弗羅貝尼烏斯多項式是另一個跟多項式環相關的環,此環的乘法...
由於推廣數系而得出四元數代數,隨之產生出實數域與複數域上的結合代數的概念,最初曾稱之為:“超複數系”。實數域上有限維可除代數有三個而且只能有此三個:實數域、複數域、四元數代數。這就是著名的弗羅貝尼烏斯定理。而韋德伯恩定理則刻畫了關於有限域的情形:有限域上有限維可除代數只能是有限域。域K上一切...
弗羅貝尼烏斯互反定理言明:若V,W分別為G,H的表示,則有自然的同構。換言之:為一對伴隨函子。若以特徵標表之,上述同構化為一個較弱但較具體的等式。例子 任意一個群G都自然地作用在其群代數上,稱為正則表現。 對稱群Sn以作用在上。 以作用於m次調和多項式上。與物理學的關係 迄今已知的物理定律通常在...
赫爾德和若爾當還建立了在有限群中的若爾當一霍爾德合成群列和若爾當一霍爾德定理。在19世紀末,德國數學家弗羅貝尼烏斯、迪克和英國數學家伯恩塞德等都致力於可解群的研究。20世紀初伯恩塞德證明的關於 (p,q是素數)必是可解群的定理,導致了對有限單群進行分類的重要研究。美國數學家湯普森和菲特在20世紀60年代初...
求出F,a₂,…,aₛ的最佳值 ɡ,a₂,…,aₛ就是弗羅貝尼烏斯問題。二元一次不定方程及其求解 設a,b,c是整數,形如ax+by=c的方程是二元一次不定方程。定理2 設a,b,c是整數,方程ax+by=c若有解(x₀,y₀),則它的一切解具有 的形式,其中 。定理1和定理2說明了解二元一次不定方程的...
的線性變換來表示。他的工作在19世紀末至20世紀初由弗羅貝尼烏斯和伯恩塞德等人推廣到一切有限抽象群的表示之中。弗羅貝尼烏斯對有限群引進了可約和完全可約表示的概念,而且證明了一個正則表示(正則表示的概念由美國數學家C.S.皮爾斯在1879年引進) 包含所有不可約表示。他在1897-1910年間還證明了許多其他結果。例...
