廣義連續統假設簡稱GCH,連續統假設的推廣,是對一般無窮基數的冪的一種假設。它可以敘述為:對任何無窮集合A,不存在集合的勢大於A的勢而小於冪集P(A)的勢。廣義連續統假設在 ZF系統中是不可判定的。
基本介紹
- 中文名:廣義連續統假設
- 外文名:generalized continunnm hypothesis(GCH)
- 適用範圍:數理科學
定義
性質
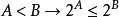


廣義連續統假設簡稱GCH,連續統假設的推廣,是對一般無窮基數的冪的一種假設。它可以敘述為:對任何無窮集合A,不存在集合的勢大於A的勢而小於冪集P(A)的勢。廣義連續統假設在 ZF系統中是不可判定的。
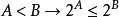

廣義連續統假設簡稱GCH,連續統假設的推廣,是對一般無窮基數的冪的一種假設。它可以敘述為:對任何無窮集合A,不存在集合的勢大於A的勢而小於冪集P(A)的勢。廣義...
1874年格奧爾格·康托爾猜測在可列集基數和實數基數之間沒有別的基數,這就是著名的連續統假設。它又被稱為希爾伯特第一問題,在1900年第二屆國際數學家大會上,...
連續統假設與廣義連續統假設是否成立?如果成立,如何證明,這曾是集合論中的一個大問題。希爾伯特在1900年的國際數學家大會上提出的23個未解決的數學問題,作為今後...
更一般的,任給定無窮基數a,在a和2a之間是否有別的基數?這稱為廣義連續統假設。數學家證明了這樣一個事實:連續統假設無法在ZFC集合論公理下被證明或證偽,換而言...
連續統假設及廣義連續統假設反映了最理想的大基數產生的方法,也就是一個接一個由冪集的基數產生出來。但是,這種理想的情況無法證明,而與它不同或矛盾的情形也不...
廣義連續統假設,就是對所有無窮基數 ,都不存在界乎 與 之間的基數。參考資料 1. 李娜.基於哲學邏輯的集合論研究:浙江大學學報(人文社會科學版),2017 ...
在廣義連續統假設成立時,每個弱不可達基數也是強不可達的。這時這兩個概念是相同的。在ZFC系統中不能證明不可達基數的存在性。稱這種基數為不可達的原因是它不...
在阿列夫數之間有沒有什麼超限數?比如說,有沒有一個數比阿列夫零大、比阿列夫1小?康托確信不存在這種數。他的猜測成為著名的廣義連續統假設。...
(R.M.Solovay)於1974年用力迫法證明了:若κ是強緊基數,對於每個>κ的奇異強極限基數λ,有2λ=λ+,亦即對於一些很特殊的、很大的基數,證明了廣義連續統假設...
奇異基數假設比廣義連續統假設弱。但和廣義連續統假設一樣,奇異基數假設探討連續統函式的取值,並猜測它總是取到最小的可能值。現代集合論的研究表明,在某種大基數...
10.在廣義連續統假設成立時 [2] :參考資料 1. 李志才主編.方法論全書 一 哲學邏輯學方法:南京大學出版社,2000年03月第1版:第328頁 2. 數學辭海編輯委員會...
可構造性公理(axiom of constructibility)是集合論的一條重要公理,該公理斷言:所有集合都是可構造的。哥德爾(K.Gödel)為了證明連續統假設與ZFC是相容的,在1939...
要么是二值可測基數。於是可推知,在廣義連續統假設下,實值可測基數與二值可測基數相同。利用以色列學者索洛韋(R.M.Solovay)於1971年的結果可以證明,實值可測...
成立,每一基數都有後繼基數,但極限基數與 沒有前行基數,在廣義連續統假設下, 的後繼基數 =2 。後繼基數相關概念 編輯 後繼基數極限基數 極限基數是一種不可數...
拉姆齊基數,則V≠L,即可構造公理不真;若存在強緊基數κ,則V≠L[X]對任何集合X成立,又對於任何大於κ的奇異強極限基數λ,2λ=λ+,這對廣義連續統假設做出了...
若承認廣義連續統假設,則可進一步以超積描述實封閉域的性狀[3] 。參考資料 1. Bob F. Caviness, Jeremy R. Johnson, editors, Quantifier elimination and ...
(R.M.Solovay)於1974年用力迫法證明了:若κ是強緊基數,對於每個>κ的奇異強極限基數λ,有2λ=λ+,亦即對於一些很特殊的、很大的基數,證明了廣義連續統假設...
由於任何基數λ的後繼基數λ不超過λ的冪2,所以每個強不可達基數必為弱不可達基數;又由於在廣義連續統假設GCH之下,λ+=2λ,所以在GCH之下,每個弱不達基數也是...
3年以後又證明了(廣義)連續統假設的相容性定理,並於1940年發表。他的工作對公理集合論有重要影響,而且直接導致了集合和序數上的遞歸論的產生。此外,哥德爾還從事...
當α是極限序數時,α=ωα=sup{ωβ|β<α};當α不是極限序數時,α是一個後繼基數。在廣義連續統假設下,α=2。基數有下列性質: [3] 1.對任何基數α,...
選擇公理相對於ZF系統的協調性以及連續統假設(包括廣義連續統假設)相對於ZFC系統的協調性正是利用這種方法獲得的.另外許多重要的組合原則、大基數性質及一些拓撲學...
