實閉域是一類重要的實域。設F是一個實域,若F的任何真代數擴張都不再是實域,則稱F是實閉的,或者F是一個實閉域。
基本介紹
- 中文名:實閉域
- 外文名:real closed field
- 學科:數理科學
- 類型:實域
- 別名:塔爾斯基原則(或定理)
定義

形式實域
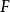
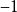


實封閉域
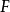







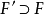



實閉包
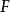



例子

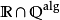
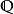
模型論觀點
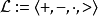

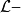

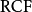










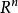

實閉域是一類重要的實域。設F是一個實域,若F的任何真代數擴張都不再是實域,則稱F是實閉的,或者F是一個實閉域。

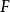
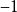


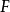







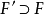



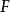




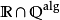
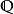
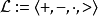

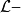











實閉域是一類重要的實域。設F是一個實域,若F的任何真代數擴張都不再是實域,則稱F是實閉的,或者F是一個實閉域。...
實代數集(real algebraic set)是坐標域為實閉域的代數集。...... 實代數集(real algebraic set)是坐標域為實閉域的代數集。設R是一個實閉域,RCX} }Xz,.....
極大序域(maximally ordered field)一種特殊的序域.指在一定意義下與實閉域等價的域.除自身外,無其他代數序擴張的序域,稱為極大序域.實閉域關於它惟一的序...
全書共分8章,論述大整數和多項式的表示與基本運算、結式與子結式、模方法與多項式的最大公因子、p進方法與多項式的因子分解、特徵列方法、Grobner基方法和實閉域...
遺傳歐氏域(hereditarily Euclidean field)歐氏域的子類一個歐氏域F,若它的每個為實域的代數擴張都是歐氏域,則稱F是遺傳歐氏域.F成為遺傳歐氏域,若且唯若F和它...
斐斯特定理(Pfister theorem)希爾伯特第17問題的定量解答.這個定理斷言:實閉域F上的n元半正定多項式,都能表為F上至多2”個有理函式的平方和.希爾伯特(Hilbert, D...
有理位存在蘭定理(Lang theorem on exis-tence of rational places)實函式域上有關實位存在性的重要結論.若F是實閉域R上的一個實函式域,x是F中有限個元素,...
阿廷定理(Artin theorem)實閉域上的多元多項式的重要定理.希爾伯特第17問題的正面解答和推廣.設F是一個實閉域,n為任一自然數,f(x)若對於F中任何一組元(a aZ...
5.代數封閉域的理論. 6.實閉域的理論. 7.阿貝爾群的理論. 8.有序阿貝爾群的理論. 9.布爾代數的理論. 10.自由群的理論. 11.歐氏幾何的理論. 12.雙曲幾何...
2.7實閉域76ii樹和偏序理論的模型論研究第三章幾個定理的新證明843.1完全k叉樹的量詞消去853.2完全無窮叉樹的量詞消去923.3完全稠密二叉偏序的量詞消去97...
全書共分8章,論述大整數和多項式的表示與基本運算、結式與子結式、模方法與多項式的最大公因子、p進方法與多項式的因子分解、特徵列方法、Grobner基方法和實閉域...
阿廷-蘭同態定理(Artin-Lang homomorphismtheorem)有理位存在的蘭定理的推廣.它在實域理論與實代數幾何中有廣泛的套用.設A是一個在實閉域R上有限生成的整環.若...
蘭嵌入定理(Lang imbedding theorem)關於域中嵌人的命題.它是蘭(Lang , S.)所獲得的一個有關實函式域的重要結果.若K是域F上一個超越次數為n的函式域,E是...
半代數集(semialgebraic set)實代數幾何中特有的術語.它給出比實代數集更廣泛的一類集合.設R是一個實閉域,RCX,}XZ,...}X」是R上n元多項式環.對於.f,}....
第二章至第九章分別介紹代數模型論各主要領域在近二三十年來國外的主要研究成果和研究方法,其中包括代數閉域、實閉域、線性序和偏序結構的模型論等。最後一章介紹...
n畢達哥拉斯域(n-Pythagorean field)高層畢達哥拉斯域.它是出自於對域元素的2n次冪所組成的集合的加法封閉性的考慮.設n為一自然數一個實域F稱為n畢達哥拉...
塔爾斯基方法(Tarski method)第一個初等代數和初等幾何命題的判定算法.195。年,塔爾斯基(Tarski , A.)證明實閉域的初等代數問題是可判定的,由此推知,初等實幾何...
