餘弦定理(廣勾股定理)

餘弦定理

廣勾股定理一般指本詞條

餘弦定理，歐氏平面幾何學基本定理。餘弦定理是描述三角形中三邊長度與一個角的餘弦值關係的數學定理，是勾股定理在一般三角形情形下的推廣，勾股定理是餘弦定理的特例。餘弦定理是揭示三角形邊角關係的重要定理，直接運用它可解決一類已知三角形兩邊及夾角求第三邊或者是已知三個邊求三角的問題，若對餘弦定理加以變形並適當移於其它知識，則使用起來更為方便、靈活。

基本介紹

公式含義,餘弦定理表達式1,驗證推導,《欽定四庫全書》上的證明,無字證明,平面幾何法證明一,平面幾何法證明二,利用正弦定理證法,平面向量證法,定理套用,求邊,求角,求面積,判定定理,判定定理一 兩根判別法,判定定理二 角邊判別法,套用例題,例如：,再如：,

公式含義

對於任意三角形，任何一邊的平方等於其他兩邊平方的和減去這兩邊與它們夾角的餘弦的積的兩倍。
若三邊為a，b，c 三角為A（
），B（
），C（
），則如下圖所示，在△ABC中，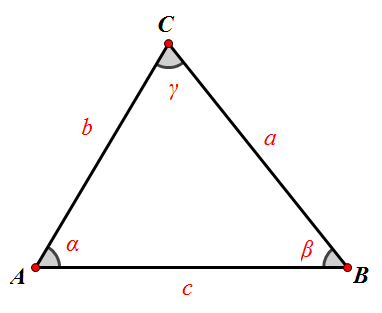
三角形三角形

餘弦定理表達式1

同理，也可描述為：
勾股定理是餘弦定理的特例，當
為90°時，
，餘弦定理可簡化為
，即勾股定理。
餘弦定理表達式2
餘弦定理表達式3（角元形式）

驗證推導

餘弦定理的歷史可追溯至西元三世紀前歐幾里得的幾何原本，在書中將三角形分為鈍角和銳角來解釋，這同時對應現代數學中餘弦值的正負。

《欽定四庫全書》上的證明

和《幾何原本》上勾股定理的證明類似。
餘弦定理餘弦定理

無字證明

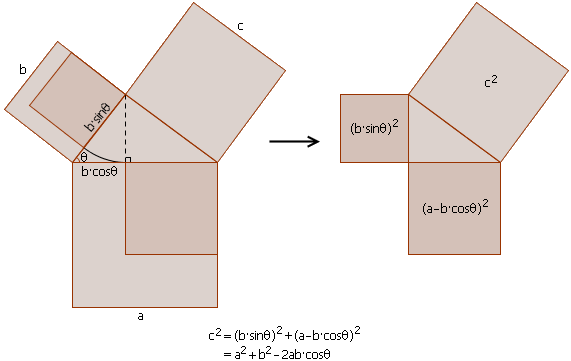
勾股定理可以推廣到餘弦定理。餘弦定理和勾股定理一樣，都有著很多不同的證明。下圖就是餘弦定理的一個無字證明。
餘弦定理的無字證明餘弦定理的無字證明

平面幾何法證明一

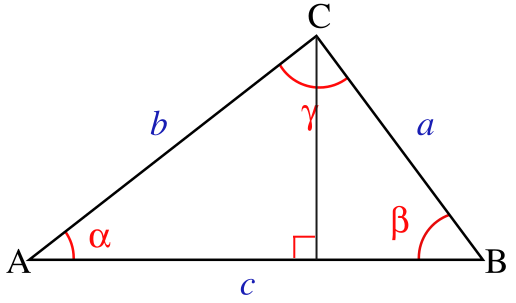平面幾何法證明平面幾何法證明
如上圖所示，△ABC，在c上做高，將c邊寫：
將等式同乘以c得到：
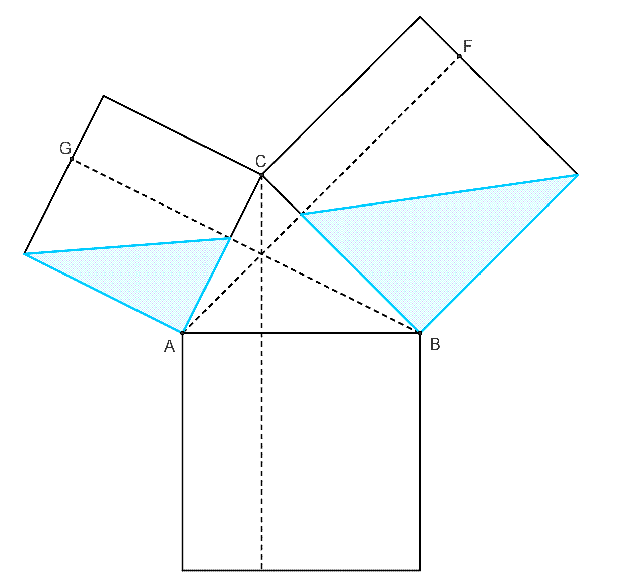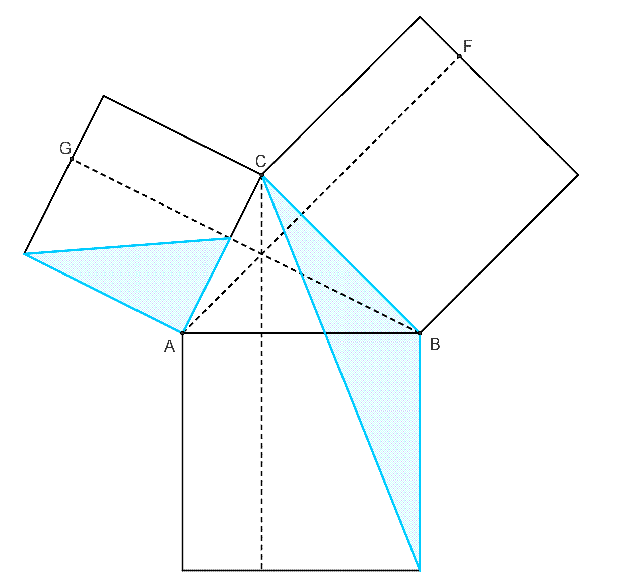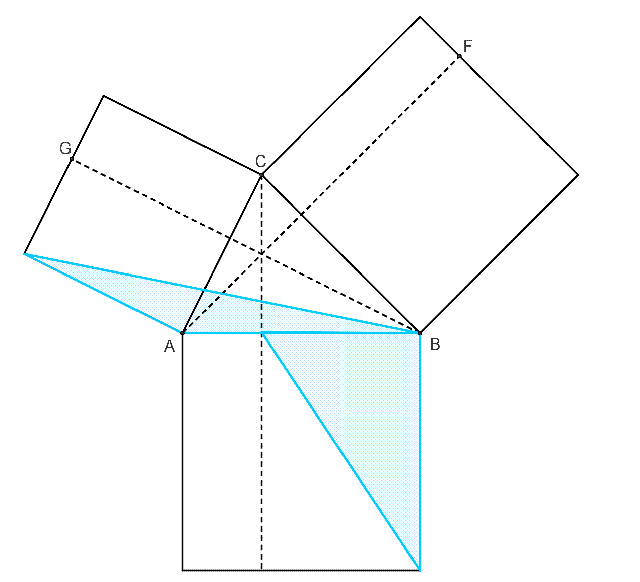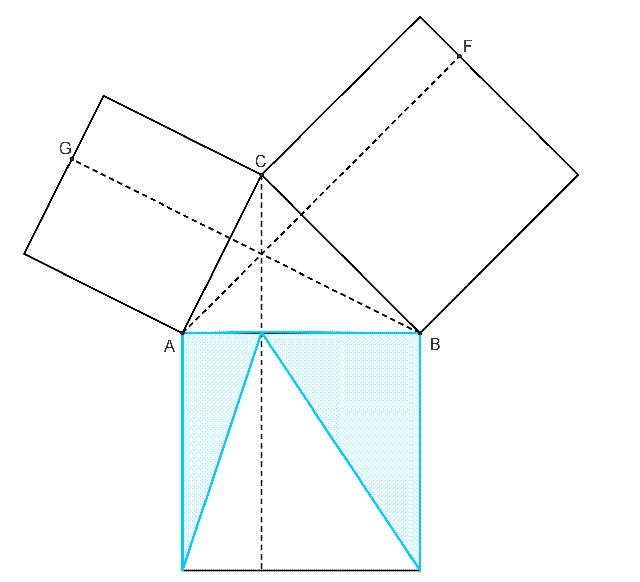
如下圖所示：以AB邊為邊長，以垂直於面ABC作向里的正方形AA`BB`輔助線，然後作平行於AA`邊的CC`等，則，上述公式相當於輔助正方形的面積等於長方形AA`C`C和BB`C`C在正方形AA`BB`中的投影面積（分別為
與
）之和。
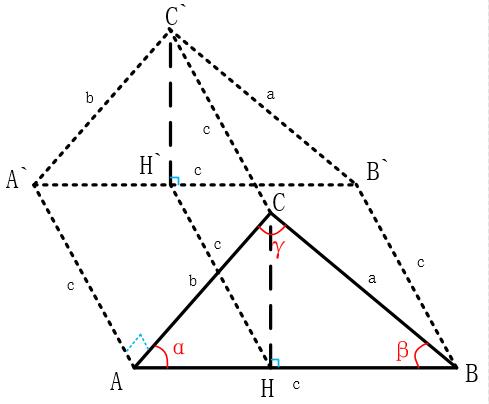立體幾何輔助說明立體幾何輔助說明
對另外兩邊分別作高，運用同樣的方法可以得到：
將兩式相加：

平面幾何法證明二

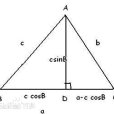
如圖所示，在△ABC中，BC=a，AC=b，AB=c，作AD⊥BC於D，則AD=c*sinB，DC=a-BD=a-c*cosB
在Rt△ACD中，
b=AD+DC=（c*sinB）+（a-c*cosB）
=csinB+a-2ac*cosB+ccosB
=c（sinB+cosB）+a-2ac*cosB
=c+a-2ac*cosB
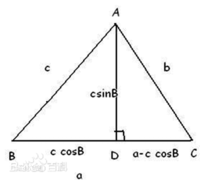平面幾何法證明二平面幾何法證明二

利用正弦定理證法

在△ABC中，
sinA+sinB-sinC
=[1-cos（2A）]/2+[1-cos（2B）]/2-[1-cos（2C）]/2（降冪公式）
=-[cos（2A）+cos（2B）]/2+1/2+1/2-1/2+[cos（2C）]/2
=-cos（A+B）cos（A-B）+[1+cos（2C）]/2（和差化積）
=-cos（A+B）cos（A-B）+cosC（降冪公式）
=cosC*cos（A-B）-cosC*cos（A+B）（∠A+∠B=180°-∠C以及誘導公式）
=cosC[cos(A-B)-cos（A+B）]
=2cosC*sinA*sinB（和差化積）（由此證明餘弦定理角元形式）
設△ABC的外接圓半徑為R
∴（RsinA）+（RsinB）-（RsinC）=2（RsinA）*（RsinB）*cosC
∴a+b-c=2ab*cosC（正弦定理）
∴c=a+b-2ab*cosC

平面向量證法

∵如圖，有a+b=c（平行四邊形定則：兩個鄰邊之間的對角線代表兩個鄰邊大小）
∴c·c=（a+b）·（a+b）
∴c=a·a+2a·b+b·b∴c=a+b+2|a||b|cos（π-θ）
（以上粗體字元表示向量）
又∵cos（π-θ）=-cosθ（誘導公式）
∴c=a+b-2|a||b|cosθ
此即c=a+b-2abcosC
即cosC=（a+b-c）/2*a*b
同理可證其他，而下面的cosC=（a+b-c）/2ab就是將cosC移到左邊表示一下。
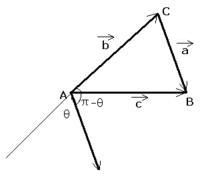平面向量證法平面向量證法

定理套用

餘弦定理是解三角形中的一個重要定理，可套用於以下三種需求：
  • 當已知三角形的兩邊及其夾角，可由余弦定理得出已知角的對邊。
  • 當已知三角形的三邊，可以由余弦定理得到三角形的三個內角。
  • 當已知三角形的三邊，可以由余弦定理得到三角形的面積。

求邊

餘弦定理公式可變換為以下形式：
因此，如果知道了三角形的兩邊及其夾角，可由余弦定理得出已知角的對邊。

求角

因為餘弦函式在
上的單調性，可以得到：
因此，如果已知三角形的三條邊，可以由余弦定理得到三角形的三個內角。

求面積

由面積公式
知如果已知三角形的三條邊，可以由余弦定理求出一個內角，從而得到三角形的面積。

判定定理

判定定理一 兩根判別法

若記m（c1,c2）為c的兩值為正根的個數，c1為c的表達式中根號前取加號的值，c2為c的表達式中根號前取
減號的值。
①若m（c1,c2）=2,則有兩解；
②若m（c1,c2）=1,則有一解；
③若m（c1,c2）=0,則有零解（即無解）。
注意：若c1等於c2且c1或c2大於0，此種情況算到第二種情況，即一解。

判定定理二 角邊判別法

一、當a>bsinA時：
①當b>a且cosA>0（即A為銳角）時，則有兩解；
②當b>a且cosA直角或鈍角）時,則有零解（即無解）；
③當b=a且cosA>0（即A為銳角）時，則有一解；
④當b=a且cosA
⑤當b
二、當a=bsinA時：
①當cosA>0（即A為銳角）時,則有一解；
②當cosA
三、當a

套用例題

例如：

已知△ABC的三邊之比為5：4：3，求最大的內角。
解：設三角形的三邊為a,b,c且a:b:c=5:4:3.
由三角形中大邊對大角可知：∠A為最大的角。
由余弦定理：
cosA=0
所以∠A=90°。

再如：

△ABC中,AB=2，AC=3，角A為60度，求BC之長。
解：由余弦定理可知：
=4+9-2×2×3×cos60
=13-12x0.5
=7
所以
（cos60°=½）
以上兩個小例子簡單說明了餘弦定理的作用。

相關詞條

熱門詞條

聯絡我們