基本介紹
- 中文名:平面正交變換
- 外文名:plane orthogonal transformation
- 所屬學科:數學
- 所屬問題:高等幾何(仿射幾何)
- 別名:保距變換,等距變換
定義
性質
































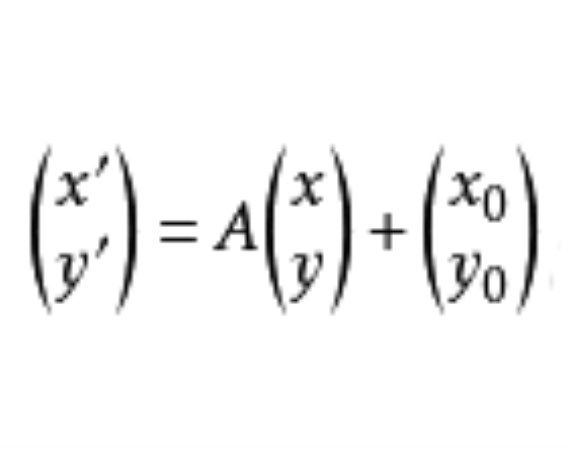
































平面上的一個點變換(點變成點的變換),如果保持點之間的距離不變,則稱它為正交變換(或等距變換),正交變換具有眾多性質,比如正交變換的乘積是正交變換,恆等變換是正交變換等。定義平面的一個點變換,如果保持點之間的距離不變。則...
契約變換(congruent transformation)是指在平面到自身的一一變換下,任意線段的長和它的像的長總相等,這種變換也叫做全等變換,或稱契約變換。契約變換也是高等代數矩陣理論中基本的交換。簡介 契約變換,亦稱全等變換或正交變換,是歐氏幾何中的一類重要變換,即使圖形變為其全等圖形的變換。如果歐氏平面(平面幾何)或...
正交變換群(orthogonal transformation group)亦稱運動群或度量群,簡稱正交群,是一類基本的變換群,即全體正交變換所構成的變換群。例如,平面上全體正交變換的集合構成平面上的正交群,空間中正交變換的全體構成空間中的正交群,平面上(空間中)的正交群是平面上(空間中)仿射群的子群,研究正交群下不變性質與不變數的...
吉文斯變換(Givens transformation)亦稱平面旋轉變換.數值代數的基本工具之一它是一種正交變換.定義 吉文斯變換(Givens transformation)亦稱平面旋轉變換.數值代數的基本工具之一它是一種正交變換.該變換為形如 的矩陣,其中:=cosB,.s=sing.(用G<i,k,B)作用在一個向量x上只改變它的第i個分量和第k個分量.最...
這也就是說,正交變換保持向量的長度不變,也保持兩個向量之間的角度不變。歐幾里得空間的例子 在二維或三維的歐幾里得空間中,兩個向量正交若且唯若他們的點積為零,即它們成90°角。可以看出正交的概念正是在此基礎上推廣而來的。三維空間中,一條直線的正交子空間是一個平面,反之亦然。四維空間中,一條直線的...
相似變換把一個圖形變為與它相似的圖形。與相似變換群相對應的幾何學稱為相似幾何學或拋物幾何學。正交變換群 亦稱運動群或度量群。簡稱正交群。一類基本的變換群。即全體正交變換所構成的變換群。例如,平面上全體正交變換的集合構成平面上的正交群,空間中正交變換的全體構成空間中的正交群。平面上(空間中)的正交...
在歐氏平面或歐氏空間中,把任一點映成與一個給定的點S對稱的點A′的變換稱為關於點S的中心反射變換,點S稱為反射中心或對稱中心。在中心反射下,連結每一對對應點A,A′所得的線段被點S所平分,反射中心S是惟一的不動點,平面上的中心反射是第一種正交變換,空間的中心反射是第二種正交變換。在平面(空間)...
軸反射變換(axial reflection transformation)簡稱軸反射,是歐氏幾何中一種重要變換。在歐氏平面上或歐氏空間中,把任一點A映成關於給定直線S對稱的點A′的變換稱為關於直線S的軸反射變換,直線S稱為反射軸。平面軸反射是第二種正交變換,空間軸反射變換亦稱半周旋轉,它是旋轉角為π的空間繞反射軸的旋轉,因而是第...
由有限次中心射影的積定義的兩條直線間的一一對應變換稱為一維射影變換。由有限次中心射影的積定義的兩個平面之間的一一對應變換稱為二維射影變換。因為正交變換、相似變換、仿射變換都保持共線三點的單比不變,必然保持共線四點的交比不變,所以這些變換都是射影變換。如果平面上點場的點建立了一個一一對應,並且...
鏡面反射變換(mirror reflection transformation)簡稱鏡面反射或平面反射,歐氏空間中的一種特殊變換。在歐氏空間中,把任一點A映成關於給定平面π對稱的點A′的變換稱為關於平面π的鏡面反射變換,平面π稱為反射平面。鏡面反射是第二種正交變換,在鏡面反射變換下,連結變換的每一對對應點A,A′所得到的線段都垂直於...
空間軸反射變換(axial reflection transformation in space)也稱“空間軸對稱變換”、“空間軸對稱”、“半周旋轉”,是一種特殊的幾何變換,是一種軸反射變換,且是第一種正交變換,指的是空間任一點變為關於同一直線的對稱點的變換。基本介紹 軸反射變換簡稱軸反射,是歐氏幾何中一種重要變換。在歐氏平面上或歐氏...
簡稱旋轉。歐氏幾何中的一種重要變換.即在歐氏平面上(歐氏空間中),讓每一點P繞一固定點(固定軸線)旋轉一個定角,變成另一點P′,如此產生的變換稱為平面上(空間中)的旋轉變換。此固定點(固定直線)稱為旋轉中心(旋轉軸),該定角稱為旋轉角。旋轉是第一種正交變換。發音:旋(xuán)轉(zhuàn)。英文:rotation...
旋轉變換簡稱旋轉,是歐氏幾何中的一種重要變換,即在歐氏平面上(歐氏空間中),讓每一點P繞一固定點(固定軸線)旋轉一個定角,變成另一點P′,如此產生的變換稱為平面上(空間中)的旋轉變換,此固定點(固定直線)稱為旋轉中心(旋轉軸),該定角稱為旋轉角。旋轉是第一種正交變換,在平面直角坐標系中,若旋轉中心...
相關概念——變換群 變換群是幾何學研究的重要對象。即由變換構成的群。設G是集合S的一一變換所構成的集合,若它滿足:1.集合內任二變換之積仍屬於這集合;2.集合內任一變換的逆變換仍屬於這集合,則稱G為S的一個變換群。例如,平面上正交變換的全體構成的變換群稱為正交群;平面上仿射變換的全體構成的變換群...
運動群亦稱正交變換群或度量群。簡稱正交群。一類基本的變換群。即全體正交變換所構成的變換群。例如,平面上全體正交變換的集合構成平面上的正交群,空間中正交變換的全體構成空間中的正交群。平面上(空間中)的正交群是平面上(空間中)仿射群的子群。研究正交群下不變性質與不變數的幾何稱為歐氏幾何或度量幾何。變換...
《解析幾何》是2008年北京大學出版社出版的圖書,作者是丘維聲。內容簡介 《解析幾何(第2版)》是北京大學數學系解析幾何課程的教材。主要講述解析幾何的基本內容和基本方法,包括:向量代數、空間直線和平面、常見曲面、坐標變換、二次曲線方程的化簡、正交變換、仿射變換、射影平面和射影變換等。《解析幾何(第2版)》...
9.5 曲面的表示 切平面 參數變換 9.6 曲面的第一基本形式 9.7 曲面上曲線的法曲率 曲面的第二基本形式 習題 第10章 平面正交變換 仿射變換 射影變換 10.1 平面正交變換 10.2 平面的仿射變換 10.3 射影平面與齊次坐標 10.4 射影映射和射影變換 習題 第11章 非歐幾何學簡介 11.1 球面幾何 11.2 雙曲...
對各章節進行適當改寫,增加適量內容及套用實例,使更貼切課堂教學實際,更方便學生自學。圖書目錄 第一章 向量代數 第二章 空間的平面和直線 第三章 常見曲線 第四章 坐標變換 第五章 二次曲線方程的化簡及其性質 第六章 正交變換和仿射變換 第七章 射影平面和它的仿射變換 ...
第10章 平面正交變換 仿射變換 射影變換 348 10-1 學時安排的建議 348 10-2 基本要求 348 10-3 內容綜述與分析 348 10-4 例題分析與解答 354 10-5 習題提示與解答 361 第11章 非歐幾何學簡介 375 11-1 學時安排的建議 375 11-2 內容提要 375 11-3 內容注析 377 附錄...
供讀者練習。圖書目錄 前言 第1章 向量代數 第2章 平面與直線 第3章 常見二次曲面 第4章 二次曲線和二次曲面的分類與方程的簡化 第5章 正交變換與仿射變換 第6章 平面射影幾何簡介 第7章 模擬考題 附錄1 深入思考與加強提高參考答案 附錄2 模擬考題參考答案 參考文獻 ...
其中,平面σ叫做對稱平面,平面對稱變換又叫做平面反射、鏡面反射變換,簡稱鏡面反射或平面反射。歐氏空間中的一種特殊變換,在歐氏空間中,把任一點A映成關於給定平面π對稱的點A′的變換稱為關於平面π的鏡面反射變換,平面π稱為反射平面,鏡面反射是第二種正交變換,在鏡面反射變換下,連結變換的每一對對應點A,...
例如,利用圓和橢圓仿射等價的事實可以得到仿射變換的重要定理:平面上的仿射變換可以分解為一個正交變換和兩個在互相垂直方向上的壓縮(或伸長)的乘積。仿射變換 由有限次中心射影的積定義的兩條直線間的一一對應變換稱為一維射影變換。由有限次中心射影的積定義的兩個平面之間的一一對應變換稱為二維射影變換。因為正交...
§1 點變換 §2 剛體運動和正交變換 §3 仿射變換 習題 附錄Ⅰ 二次曲線的一般理論 §1 坐標變換 §2 在坐標變換下二次方程係數的變換 §3 二次曲線方程的化簡 §4 二次曲線的類型和形狀的判別 §5 二次曲線的位置的確定 §6 不變數的概念 習題 附錄Ⅱ 射影幾何初步 §1 射影平面 §2 射影空間 §3 ...
4.1 空間坐標變換 4.2 二次曲面的化簡 4.3 二次曲面的分類 4.4 二次曲面的不變數 4.5 二次曲面的中心與漸近萬向 4.6 二次曲面的主徑面、奇向 4.7 二次曲面的切平面 4.8 平面二次曲線 第5章 正交變換和仿射變換 5.1 變換與變換群 5.2 正交變換 5.3 仿射變換 第6章 平面射影幾何簡介 6.1...
第3章討論空間直角坐標系中用一次方程表示的圖形(直線與平面)。第4、5章主要討論空間直角坐標系中用二次方程表示的曲面(二次曲面)。第6、7章簡單介紹了正交變換與仿射變換,以及射影幾何基礎。圖書目錄 目錄 第1章 空間坐標系與向量代數 1.1 空間直角坐標系 1.2 曲面和曲線的方程 1.3 向量的概念與向量的線性...
第3章討論空間直角坐標系中用一次方程表示的圖形(直線與平面)。第4、5章主要討論空間直角坐標系中用二次方程表示的曲面(二次曲面)。第6、7章簡單介紹了正交變換與仿射變換,以及射影幾何基礎。作為一學期每周4學時(3小時講授,1小時習題課)用的教材,本書配置有適量的習題。第7章射影幾何部分可酌情講授或刪...
旋轉變換簡稱旋轉,是歐氏幾何中的一種重要變換,即在歐氏平面上(歐氏空間中),讓每一點P繞一固定點(固定軸線)旋轉一個定角,變成另一點P′,如此產生的變換稱為平面上(空間中)的旋轉變換,此固定點(固定直線)稱為旋轉中心(旋轉軸),該定角稱為旋轉角。旋轉是第一種正交變換,在平面直角坐標系中,若旋轉中心...
