基本介紹
- 中文名:正交變換群
- 外文名:orthogonal transformation group
- 所屬學科:數學
- 所屬問題:高等幾何(幾何基礎)
- 別名:運動群或度量群
- 簡稱:正交群
- 簡介:全體正交變換所構成的變換群
基本介紹










正交變換群的幾何—歐氏幾何
相關概念



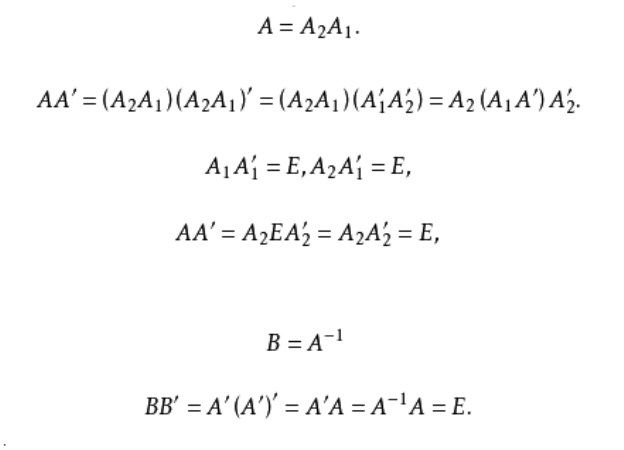















正交變換群(orthogonal transformation group)亦稱運動群或度量群,簡稱正交群,是一類基本的變換群,即全體正交變換所構成的變換群。例如,平面上全體正交變換的集合構成平面上的正交群,空間中正交變...
為正交矩陣,則 稱為正交表示。有限群在實數域上的任意的矩陣表示都等價於一個正交表示。正交變換 線上性代數中,正交變換是線性變換的一種,它從實內積空間V映射到V自身,且保證變換前後內積不變。因為向量的模長與夾角都是用內積定義...
平面上的一個點變換(點變成點的變換),如果保持點之間的距離不變,則稱它為正交變換(或等距變換),正交變換具有眾多性質,比如正交變換的乘積是正交變換,恆等變換是正交變換等。定義 平面的一個點變換,如果保持點之間的距離不變。則...
平移是第一種正交變換。平移變換的逆變換也是平移變換,兩個平移變換的乘積仍是平移變換。所有平移變換的全體構成一個群,稱為平移群。平移變換的概念可以推廣到n維歐氏空間。對稱變換 定義 若一個平面圖形K在平面剛體運動m的作用下仍與...
空間旋轉變換(rotation transformation in space)是一種特殊的幾何變換,指空間的所有點繞同一直線旋轉同一角度的變換,亦稱特徵正交變換,是一種特殊的正交變換,n維歐氏空間正交變換的行列式只能是1或-1,行列式等於1的正交變換稱為旋轉變換...
按照變換群的觀點,幾何學可以這樣分類:研究射影變換群、仿射變換群、相似變換群、正交變換群下不變性質和不變數的幾何學分別是射影幾何學、仿射幾何學、拋物幾何學、歐氏幾何學.正交變換群也稱為運動群,歐氏幾何學的主要內容就是研究...
按照變換群的觀點,幾何學可以這樣分類:研究射影變換群、仿射變換群、相似變換群、正交變換群下不變性質和不變數的幾何學分別是射影幾何學、仿射幾何學、拋物幾何學、歐氏幾何學。正交變換群也稱為運動群,歐氏幾何學的主要內容就是研究...
這種觀點突出了變換群在研討幾何中的地位,為用近代數學方法研究幾何學開闢了道路,因此後來把它簡稱為《埃爾朗根綱領》。按照變換群的觀點,幾何學可以這樣分類:研究射影變換群、仿射變換群、相似變換群、正交變換群下不變性質和不變數的...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。運動群亦稱正交變換群或度量群。簡稱正交群。一類基本的變換群。即全體正交變換所構成的變換群。雙曲運動群(hyperbolic motion group)一種運動...
變換群是幾何學研究的重要對象。即由變換構成的群。設G是集合S的一一變換所構成的集合,若它滿足:1.集合內任二變換之積仍屬於這集合;2.集合內任一變換的逆變換仍屬於這集合,則稱G為S的一個變換群。例如,平面上正交變換的全體...
§2 正交變換與歐氏幾何 2.1 基本概念 2.2 代數表示式 2.3 正交變換群 §3 仿射變換與仿射幾何 3.1 平面上的仿射坐標系與仿射變換 3.2 仿射變換的基本性質 3.3 仿射變換群與仿射幾何 §4 射影變換與射影幾何 4.1 齊次坐標...
並且在擴大的仿射平面(空間)中,它還是保持無窮遠直線(無窮遠平面)不變的一個射影變換群。因此,仿射群是射影群的子群,仿射幾何是射影幾何的子幾何。正交變換 一類重要的線性變換。設σ是歐氏空間V的線性變換,如果對V的任意向量α,...
