面對稱空間圖形(space figure symmetric with respect to a plane)是一種特殊的圖形，指空間圖形以一個鏡面反射變換為其自對稱變換的圖形。鏡面反射變換的反射面稱為圖形的對稱面，面對稱空間圖形可以不只一個對稱面，面對稱空間圖形上任何一點關於對稱面的對稱點都在本圖形上，且任何一雙對稱點的連線段被對稱面垂直平分。
基本介紹
- 中文名：面對稱空間圖形
- 外文名：space figure symmetric with respect to a plane
- 所屬學科：數學
- 所屬問題：空間幾何（空間變換）
- 原理：鏡面反射變換（平面對稱變換）
基本概念,三種對稱形式的關係,平面對稱(鏡面反射),
基本概念
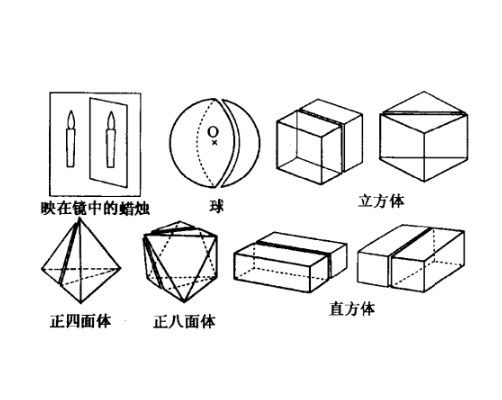
如果一個圖形經過平面對稱後所得到的圖形仍是這個圖形本身，則這個圖形叫做關於平面的自相對稱的圖形，或叫做面對稱圖形（如圖1、圖2所示）。如果一個圖形經過軸對稱後所得到的圖形仍是這個圖形本身，這個圖形叫做關於軸的自相對稱的圖形，或叫做軸對稱圖形，如果一個圖形經過中心對稱後所得到的圖形仍是這個圖形本身，則這個圖形叫做關於中心的自相對稱圖形，或叫做中心對稱圖形，這三種圖形統稱為對稱圖形。
在客觀實際中對稱圖形是一種常見的幾何圖形，例如自然界中的雪花和晶體、房屋建築、橋樑、桌子、碗、茶杯等等很多是對稱圖形，它們既美觀又實用。
三種對稱形式的關係
我們可以證明三種對稱形式之間有下面的關係．
定理1 如果直線
和平面M垂直相交於O點，一個空間圖形具有下列對稱性：
1. 關於平面M對稱；
2. 關於軸 對稱；
3. 關於中心O對稱。
中的任意兩個，則它一定具有第三個。
這個定理的意思就是在一定的條件下，如果一個圖形同時是兩種對稱圖形，那么它一定是第三種對稱圖形。
證明 下面只證明其中的一種情況，例如如果一個空間圖形關於平面M對稱，且關於中心O對稱，那么它一定關於直線 成軸對稱。其餘情況可同理推證。
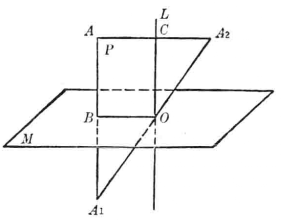
圖3
如圖3中，設A是圖形F上的任意一點，作A點關於平面M的對稱點A'，再作A1點關於O點的對稱
點A2，由於圖形F是面對稱圖形，又是中心對稱圖形，所以A1、A2都在圖形F上。
∵ ⊥平面M，AA1⊥平面M，
∴AA1// ，
AA1和 確定平面P，則O點在平面P上，
∴A1O在平面P上，A2點也在平面P上，
即A、A1、A2和 都在平面P上。
連線AA2和 交於C點，AA1與平面M交於B點，連線OB，
∵AB= A1B，OA1= OA2，
∴AA2//OB，而 ⊥OB，
∴AA2⊥ ，
又AA1// ，
∴AC= A2C，
∴A和A2關於直線 成軸對稱
平面對稱(鏡面反射)
如果圖形F和F’的對應點的連線段均被某一固定平面σ垂直平分，則稱圖形F和F’關於平面一對稱，並把從圖形F到F’的變換叫做平面對稱變換，簡稱面對稱。其中，平面σ叫做對稱平面，平面對稱變換又叫做平面反射、鏡面反射變換，簡稱鏡面反射或平面反射。歐氏空間中的一種特殊變換，在歐氏空間中，把任一點A映成關於給定平面π對稱的點A′的變換稱為關於平面π的鏡面反射變換，平面π稱為反射平面，鏡面反射是第二種正交變換，在鏡面反射變換下，連結變換的每一對對應點A，A′所得到的線段都垂直於反射平面π且被π所平分，平面π上的點都是不動點，鏡面反射變換在直觀上相當於把平面π看做一面鏡子，變換前後的對應點就好比是物與像那樣，在空間直角坐標系中，若把坐標平面xOy取為反射平面，則鏡面反射變換的代數表達式為
鏡面反射亦稱非特徵正交變換，又稱第二類正交變換，是一種特殊的正交變換。設V是歐氏空間，α是V的非零向量。對任意的β∈V，由
