基本介紹
- 中文名:平行四邊形定則
- 外文名:parallelogram law
- 別名:平行四邊形法則
- 表達式:F=F1+F2+2F1F2Cosθ
- 提出者:皮耶利·瓦里翁
- 提出時間:1726年
- 適用領域:物理
- 套用學科:數學、物理
發展簡史
數學推導





實驗驗證
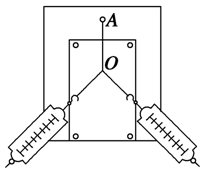
實驗目的
實驗方法


平行四邊形法則一般指本詞條








對於平面上任何一點,都存在一條能將平行四邊形平分為兩個面積相等圖形、並穿過該點的線;四邊邊長的平方和等於兩條對角線的平方和。分類 矩形、菱形、正方形是特殊的平行四邊形。判定定理 (1)定義法:兩組對邊分別平行的四邊形是平行四邊形;(2)兩組對邊分別相等的四邊形是平行四邊形;(3)兩組對角分別相等...
平行四邊形(Parallelogram),是在同一個二維平面內,由兩組平行線段組成的閉合圖形。平行四邊形一般用圖形名稱加四個頂點依次命名。註:在用字母表示四邊形時,一定要按順時針或逆時針方向註明各頂點。在歐幾里得幾何中,平行四邊形是具有兩對平行邊的簡單(非自相交)四邊形。 平行四邊形的相對或相對的側面具有相同...
的和,這種計算法則叫做向量加法的平行四邊形法則。減法運算 與 長度相等,方向相反的向量,叫做 的相反向量,,零向量的相反向量仍然是零向量。(1);(2)。以減向量的終點為起點,被減向量的終點為終點(三角形法則)。數乘運算 實數λ與向量 的積是一個向量,這種運算叫做向量的數乘,記作 ,。當λ > 0時...
點撥:經驗得知兩個分力F1、F2間夾角θ越大,用平行四邊形作圖得出的合力F的誤差也越大,所以實驗中不要把θ角取得太大,一般不大於90°為最佳。橡皮條、細繩、測力計應在同一平面內,測力計的掛鈎應避免與紙面磨擦。(3)用鉛筆記下O點的位置,畫下兩條細繩的方向,並記下兩個測力計的讀數。點撥:拉橡皮...
三角形定則是指兩個力(或者其他任何矢量)合成,其合力應當為將一個力的起始點移動到另一個力的終止點,合力為從第二個的起點到第一個的終點。性質 其實;三角形定則是平行四邊形定則的簡化。有時為了方便也可以只畫出一半的平行四邊形,也就是力的三角形法則。平行四邊形法則:它是一種共點力的合成法則.這...
力的平行四邊形法則。作用在物體同一點上的兩個力可合成一個合力,合力的作用點也在該點,大小和方向由這兩個力為邊構成的平行四邊形的對角線確定。用矢量表示為:F = F ₁+ F ₂ 作用於物體同一點上的二力可以合成為一個力(稱為合力)。合力作用點仍在該點,合力的大小和方向由以兩分力為鄰邊構成的...
1.力的合成與分解互為逆運算,都符合平行四邊形定則:如果用表示兩個共點力F1和F2的線段為鄰邊作平行四邊形,那么合力F的大小和方向就可以用F1、F2所夾的角的度數以及大小來表示。(註:已知分力要求合力,叫做力的合成。已知合力要求分力叫做力的分解。)2.力的合成與分解的法則:平行四邊形法則。即力的合成就...
力的平行四邊形法則 作用在物體上同一點的兩個力,可合成一個合力,合力的作用點仍在該點,其大小和方向由以此兩力為邊構成的平行四邊形的對角線確定,即合力等於分力的矢量和。合力的大小和方向也可通過力三角形法得到。即自任一點O以和為兩邊作力三角形,第三邊即所求。平行四邊形法則是力的合成法則,也是...
力的平行四邊形法則 作用在物體上同一點的兩個力,可合成一個合力,合力的作用點仍在該點,其大小和方向由以此兩力為邊構成的平行四邊形的對角線確定,即合力等於分力的矢量和。合力的大小和方向也可通過力三角形法得到。 即自任一點O以和為兩邊作力三角形,第三邊即所求。·此公理給出了力系簡化的基本方法...
利用力的平行四邊形法則(見靜力學公理)將共點力系各力順序合成,就可求得共點力系的合力。合力矢是力多邊形的封閉邊。這種求共點力系的幾何方法稱為力多邊形法。在特殊情況下,若共點力系各力構成的折線的終點和起點重合,即封閉邊為零,則該力系的合力為零,這時力系就成為平衡力系。平行力系的合成 各力作用線...
力的分解 (resolution of a force) 將一個力化作等效的兩個或兩個以上的分力。分解的依據是力的平行四邊形法則(見靜力學公理)。這個問題一般可有無數組解,只有在另外附加足夠條件的情況下,才能得到確定解。介紹 力的分解是力的合成的逆運算,求一個力的分力的過程。同樣遵守平行四邊形定則。將一個力化...
向量是將幾何問題轉化為代數問題的橋樑,向量的加減則是用代數方法進行幾何運算。三角形定則 三角形定則解決向量加法的方法:將各個向量依次首尾順次相接,結果為第一個向量的起點指向最後一個向量的終點。平行四邊形定則 平行四邊形定則解決向量加法的方法:將兩個向量平移至公共起點,以向量的兩條邊作平行四邊形,結果...
向量(矢量)這個術語作為現代數學-物理學中的一個重要概念,首先是由英國數學家哈密頓使用的。向量的名詞雖來自哈密頓,但向量作為一條有向線段的思想卻由來已久。向量理論的起源與發展主要有三條線索:物理學中的速度和力的平行四邊形法則、位置幾何、複數的幾何表示。物理學中的速度與力的平行四邊形概念是向量理論...
用平行四邊形法則合成一個向量,那么用於合成的那兩個向量就叫做合向量的分向量 定義 分向量,也叫分矢量,是指把一個向量分解而得到的兩個或多個向量。向量的分解遵從平行四邊形法則。引用示例 例: 向量c=m*向量a+n*向量b 分別在向量a,向量b方向上的分向量是 ma,nb。nb與ma夾角應小於等於180度 ...
n. 平行四邊形 [ 複數 parallelograms ]短語搭配 parallelogram of force 力平行四邊形 ; 力平行東南西北兒形 parallelogram rule [物] 平行四邊形定則 ; 平行四邊形定律 ; 平行四邊形法則 ; 平行四邊形定則英語 parallelogram law [數] 平行四邊形定律 ; 平行四邊形法則 ; 平行四邊形恆等式 parallelogram method...
無法則則無法形成藝術作品,而法則過於複雜必定會影響行筆之流暢。所以我認為必定存在一個簡單的結體法則供絕大多數書法家所遵循。平行四邊形法則 1、傳統法則及習字手段 在歷史上書法大家所留世的書法論述中,專講行書結體的論述並不多見,考慮到行書實為楷書的快寫之體,思考一下楷書的結體法則很有助於對行書結體...
矢量運算,矢量之間的運算要遵循特殊的法則。矢量加法一般可用平行四邊形法則。由平行四邊形法則可推廣至三角形法則、多邊形法則或正交分解法等。矢量減法是矢量加法的逆運算,一個矢量減去另一個矢量,等於加上那個矢量的負矢量。介紹 向量(英語:vector,物理、工程等也稱作矢量)是數學、物理學和工程科學等多個自然...
與還原論密切相關的另種科學方法是分析的方法。即把整體對象分解為各個因素或組成部分加以研究的方法。笛卡兒使用此法建立了解析幾何。史蒂芬創立了把力分解為兩個力合力的平行四邊形法則。伽利略和牛頓在力學上取得成功的前提,在於把複雜的運動理解為若干運動的簡單合成。它是和機械還原論密切相關的另一種科學方法。即...
利用平行四邊形法則或者三角形法則求出兩個力的合力的方法叫做二力合成。當兩個或兩個以上的力作用於一個物體時,為了方便研究物體的受力和運動,把多個力轉換為一個力,即為二力合成。當二力作用在同一直線同方向時將二力相加求出合力,方向與任意一力方向相同;不同方向時,用大力減去小力求出合力,方向與大力...
疊加遵循矢量的疊加法則——平行四邊形法則。還可以使用矢量三角形法,正交分解法等。利用電場的疊加原理,理論上可計算任意帶電體在任意點的場強。對於一個帶電的物體,在計算它的電場時,可以把它分成若干小塊,只要每個小塊足夠小,就可把每小塊所帶的電荷看成為點電荷,然後用點電荷電場疊加的方法計算整個帶電...
斯蒂文從“永久運動不可能”公設出發論證力的平行四邊形法則,他還在前人用運動學觀點解釋平衡條件的基礎上,得到虛位移原理的初步形式,為拉格朗日的分析力學提供依據。G.P. de羅貝瓦爾證明了一般情況下的平行四邊形法則。P.伐里農發展了古希臘靜力學的幾何學觀點,提出力矩的概念和計算方法(1687)並用以研究剛體平衡...
古希臘的數學家阿基米德(公元前 3世紀)提出了槓桿平衡公式(限於平行力)及重心公式,奠定了靜力學基礎。荷蘭學者S.斯蒂文(16世紀)解決了非平行力情況下的槓桿問題,發現了力的平行四邊形法則。他還提出了著名的“黃金定則”,是虛位移原理的萌芽。這一原理的現代提法是瑞士學者約翰·伯努利於1717年提出的。動力...
這些量之間的運算遵循一般的代數法則。例如溫度、質量這些物理量,這樣的量叫做物理標量。(2)說明:①矢量之間的運算要遵循特殊的法則。矢量加法一般可用平行四邊形法則。由平行四邊形法則可推廣至三角形法則、多邊形法則或正交分解法等。矢量減法是矢量加法的逆運算,一個矢量減去另一個矢量,等於加上那個矢量的負矢量...
例如,若V為三維幾何空間中全體向量(有向線段)構成的集合,P為實數域R,則V關於向量加法(即平行四邊形法則)和數與向量的乘法構成實數域R上的線性空間。又如,若V為數域P上全體m×n矩陣組成的集合M(P),V的加法與純量乘法分別為矩陣的加法和數與矩陣的乘法,則M(P)是數域P上的線性空間.V中向量就是m×...
例如,若V為三維幾何空間中全體向量(有向線段)構成的集合,P為實數域R,則V關於向量加法(即平行四邊形法則)和數與向量的乘法構成實數域R上的線性空間。又如,若V為數域P上全體m×n矩陣組成的集合M(P),V的加法與純量乘法分別為矩陣的加法和數與矩陣的乘法,則M(P)是數域P上的線性空間。V中向量就是m×n...
例如,若V為三維幾何空間中全體向量(有向線段)構成的集合,P為實數域R,則V關於向量加法(即平行四邊形法則)和數與向量的乘法構成實數域R上的線性空間。又如,若V為數域P上全體m×n矩陣組成的集合Mmn(P),V的加法與純量乘法分別為矩陣的加法和數與矩陣的乘法,則Mmn(P)是數域P上的線性空間.V中向量就是m×...
注意:標量不遵守平行四邊形法則!其它 矢量和標量的定義:(到大學物理中會詳細研究)(1)定義或解釋:有些物理量,既要有數值大小(包括有關的單位),又要由方向才能完全確定。這些量之間的運算並不遵循一般的代數法則,而遵循特殊的運算法則。這樣的量叫做物理矢量。有些物理量,只具有數值大小(包括有關的單位...
所謂合場強就是場強的矢量和 定義 所謂合場強就是場強的矢量和 遵循平行四邊形法則.比如,真空中在同一直線上的兩個等量異種電荷.其連線中點的場強就是在中點放入一個檢驗電荷,分別求檢驗電荷在兩個電場中的場強,再進行矢量運算,就是合場強了.判斷方法 合場強的判斷則應先分別搞清兩點電荷在此處產生的場強的方向,...
