基本介紹
- 中文名:常數變易法
- 外文名:A method of constant variation
- 適用範圍:數理科學
- 完成人:拉格朗日
定義

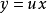
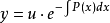
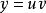










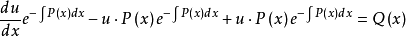
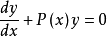
套用






































































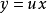
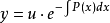
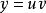










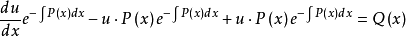
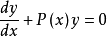




































































常數變易法是解線性微分方程行之有效的一種方法。它是拉格朗日十一年的研究成果,我們所用僅是他的結論,並無過程。...
一階線性微分方程的求解一般採用常數變易法,通過常數變易法,可求出一階線性微分方程的通解。一階線性微分方程一階齊次線性微分方程 對於一階齊次線性微分方程:...
欲得到非齊次線性微分方程的通解,我們首先求出對應的齊次方程的通解,然後用待定係數法或常數變易法求出非齊次方程本身的一個特解,把它們相加,就是非齊次方程的...
高階方程中幾乎只有少數二階方程(當用瀑布法時在一系列不變數中有一個開始為零的情形,和少數極個別的非線性方程等等)可以求得通解。線上性情形,推廣常數變易法...
瞬時橢圓法最早是歐拉在十八世紀中葉研究木星與土星的相互攝動時提出的,後由拉格朗日加以改進。他根據常數變易法,利用拉格朗日括弧,嚴格地導出了描述橢圓軌道要素變化...
形式伴隨方程(formal adjoint equation)是在Rn中為確定常數變易公式的積分核而導出的相關方程。...
瞬時橢圓法最早是歐拉在十八世紀中葉研究木星與土星的相互攝動時提出的,後由拉格朗日加以改進。他根據常數變易法,利用拉格朗日括弧,嚴格地導出了描述橢圓軌道要素變化...
對於一階線性常微分方程,常用的方法是常數變易法:對於方程:y'+p(x)y+q(x)=0,可知其通解: ,然後將這個通解代回到原式中,即可求出C(x)的值。...
他根據常數變易法,利用拉格朗日括弧,嚴格地導出了描述橢圓軌道要素變化的攝動方程──拉格朗日方程。這種方法的套用十分廣泛,特別是被勒威耶成功地用來研究大行星的運動...
如果知道了齊次方程的通解,則能通過參數變動法(或稱常數變易法,見初等常微分方程)得到非齊次方程的解。因此線性方程的中心問題是研究齊次方程,而 n 階齊次線性...
2.2 線性微分方程與常數變易法2.3 恰當微分方程與積分因子2.3.1 恰當微分方程2.3...常微分方程(第3版)編輯推薦 編輯 該書按照教學大綱的要求,較全面地...
用“常數變易法”求解。令f(t)=u(t)e-∫p(t)dt,代入方程得u(t)=∫(t)e∫p(t)dtdt+c1f(t)=c1e-∫p(t)dt+e-∫p(t)dt...
特別當n≥3,f(x)為xk,eax,cosβx,sinβx等類函式之和,或它們乘積之和時,求方程的特解較用常數變易法簡便。運算元方法類似地可運用到常係數線性常微分方程組...
若函式y1和y2之比為常數,稱y1和y2是線性相關的;若函式y1和y2之比不為常數...比較常用的求解方法是待定係數法 [2] 、多項式法、常數變易法和微分運算元法等...
§8.6 常數變易法第九章 首次積分§9.1 例子§9.2 首次積分理論§9.3 首次積分的獨立性第十章 一階擬線性偏微分方程§10.1 一階線性齊次偏微分方程...
這是一階線性微分方程,可用常數變易法或公式代入求出解來Bernoulli方程伯努利 編輯 丹尼爾伯努利(Daniel bernoulli) 1700-1782,出生於荷蘭是著名的數學家,物理學家和...
第4章 一階非齊次線性微分方程常數變易法——撥開雲霧1.現象2.模型3.解4.解釋5.常量變易法第5章 二階線性微分方程——不只是搖擺運動1.振動現象...
瞬時橢圓法最早是歐拉在十八世紀中葉研究木星與土星的相互攝動時提出的,後由拉格朗日加以改進。他根據常數變易法,利用拉格朗日括弧,嚴格地導出了描述橢圓軌道要素變化...
4.1.3 非齊次線性微分方程與常數變易法§4.2 常係數線性微分方程的解法4.2.1 復值函式與復值解4.2.2 常係數齊次線性微分方程和歐拉方程...
第一章 初等積分法 §1.1 基本概念(微分方程與解) §1.2 變數可分離方程 §1.3 齊次方程(可化為變數可分離方程) §1.4 一階線性方程與常數變易法...
一、函式單調性的判定法 一、二階線性微分方程舉例 二、曲線的凹凸性與拐點 二、線性微分方程的解的結構 習題3-4 *三、常數變易法 第五節函式的極值與最大值...
[1] ;下冊內容為多元函式微分法及其套用、重積分、曲線積分與曲面積分、無窮...*三、 常數變法 習題12-7 第八節 常係數線性方程 習題12-8 第九 常...
指導 畢業論文: 4 人,其中單小芸論文“首次積分與常數變易法 ” 被評為優秀論文; 指導數學實驗:2 屆,共 381 人次 近年 發表的主要論文: [1] Wangyuan ...
4.3 非齊次線性微分方程 常數變易法4.4 常係數線性齊次微分方程式4.5 常係數非齊次線性方程 待定係數法4.6 RLC交流電路4.7 Euler方程4.8 二階微分方程的降階法...
並揉合常數變易法、法向雙曲不變流形理論、橫截性等理論和方法,創造性地建立了一套既有著較為完整的理論體系、又非常簡潔高效的適合於研究異常困難的高維系統...
第一節 利用分離變數法和常數變易法解微分方程129 第二節 利用拉普拉斯變換解微分方程133 第三節 微分方程與數學模型137 第八章 級數143 第一節 正項級數...
