巴拿赫流形是有限維流形的無窮維推廣,巴拿赫流形一般均指巴拿赫微分流形,光滑流形一般是指C∞流形。
基本介紹
- 中文名:巴拿赫流形
- 外文名:Banach manifold
- 適用範圍:數理科學
簡介,性質,特殊巴拿赫流形,
簡介
巴拿赫流形是有限維流形的無窮維推廣。
設M是豪斯多夫拓撲空間,E是巴拿赫空間。若對於M上的每一點p,均存在p的開鄰域U與從U到E中某開集上的同胚映射φ:U→p(U)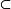 E,則稱M為以E為模的巴拿赫拓撲流形或者C0巴拿赫流形。
E,則稱M為以E為模的巴拿赫拓撲流形或者C0巴拿赫流形。
這時每個(U,φ)稱為M上的個區圖。
性質
設M是以E為模的C0巴拿赫流形,r是某個正整數或+∞,(Uα,φα)與(Uβ,φβ)是M上的兩個區圖。若Uα∩Uβ=∅,或當Uα∩Uβ≠∅時其傳遞函式 是Cr微分同胚,則稱這兩個區圖是Cr相容的。
是Cr微分同胚,則稱這兩個區圖是Cr相容的。

設D是由M上的一些區圖所成之族。若D中任意兩個成員均是Cr相容的,且D構成M的開覆蓋,則稱D為M上的一個Cr圖冊。如果M上的一個Cr圖冊D在Cr相容的意義下還是極大的,即不能在D中再添加新的成員使其仍保持Cr相容性,則稱D為M上的一個Cr微分結構。
特殊巴拿赫流形
M連同其上指定的一個Cr微分結構D,稱為以E為模的Cr巴拿赫流形,記為(M,D)。由於M上的一個C圖冊總可惟一地生成一個極大的Cr圖冊,因此當給定了M上的一個Cr圖冊D(不必極大)時,亦稱(M,D)是Cr巴拿赫流形。
C巴拿赫流形(M,ID)上的區圖指的是D中的成員。當p∈Uα時,(M,D)上的區圖(Uα,φα)亦稱為在點p處的局部坐標系。r≥1時的Cr巴拿赫流形稱為巴拿赫微分流形。如無特別說明,
巴拿赫流形一般均指巴拿赫微分流形,光滑流形一般是指C∞流形。
巴拿赫空間E本身,連同其上的一個C∞圖冊D={(E,I)}(此圖冊僅由一個成員組成,其中I為E上的恆同映射),成為一個以E為模的C∞巴拿赫流形。通常說到E是巴拿赫流形時即是在此意義下而言。
