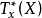所謂無限維流形,通常是指巴拿赫空間或希爾伯特空間維模型空間的微分流形。
基本介紹
- 中文名:無限維流形
- 外文名:infinite-dimensional manifold
- 適用範圍:數理科學
簡介,套用,定義圖冊,定義切向量,
簡介
無限維流形是有限維流形的推廣。
所謂無限維流形,通常是指巴拿赫空間或希爾伯特空間維模型空間的微分流形。
套用
定義圖冊
無限維流形為了適應數學研究的需要而發展起來的,除了它在維數等方面有別於普通的微分流形之外,很多概念都可以類似於有限維情形而獲得定義,例如,可以定義 類圖冊。
類圖冊。

設 X 是一個集合,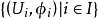 是一族區圖集,若他滿足下列條件,則稱這樣的
是一族區圖集,若他滿足下列條件,則稱這樣的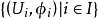 維一個
維一個 類圖冊,而每個
類圖冊,而每個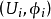 稱為該圖冊中的區圖:
稱為該圖冊中的區圖:
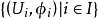
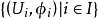

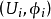
1、每個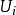 是 X 的一個子集,且
是 X 的一個子集,且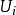 的全體覆蓋 X;
的全體覆蓋 X;
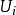
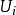
2、每個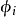 是
是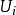 到某個巴拿赫空間 E 的開子集
到某個巴拿赫空間 E 的開子集 的雙射,且對任意 i,j,
的雙射,且對任意 i,j,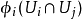 在E 中是開子集;
在E 中是開子集;
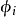
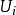

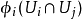
3、映射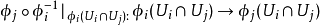 對每一對指標 i,j 是一個
對每一對指標 i,j 是一個 同構
同構
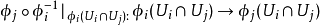

定義切向量
無限維流形也可以定義切向量:
設X是一個E流形,則在任一點 x∈X 處的切向量有兩個等價的定義:
1、在流形 X 處的切向量是在x處相切的曲線的一個等價類,即所有的曲線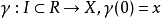 ,若在某個區圖
,若在某個區圖 中,
中,
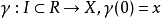

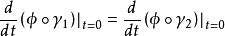
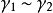
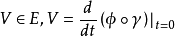

2、是x∈X 處三元組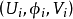 的等價類,其中
的等價類,其中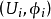 是 X 在 x 處的任一相容區圖,
是 X 在 x 處的任一相容區圖,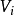 是 E 的一個向量,若
是 E 的一個向量,若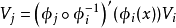 ,則三元組
,則三元組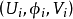 與
與 等價。
等價。
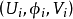
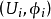
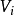
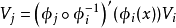
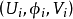

X在x處切向量的全體構成一個向量空間,稱這個向量空間為切空間,記為 ,類似地也可定義相應的餘切向量與餘切空間
,類似地也可定義相應的餘切向量與餘切空間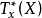 。
。