對數求導法是一種求函式導數的方法。
取對數的運算可將冪函式、指數函式及冪指函式運算降格成為乘法運算,可將乘法運算或除法運算降格為加法或減法運算,使求導運算計算量大為減少。
對數求導法套用相當廣泛。
基本介紹
- 中文名:對數求導法
- 領域:數學
- 作用:求函式導數
- 優點:求導運算計算量大為減少
定義



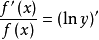

原理


適用性

求導舉例

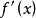




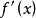



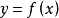











套用舉例





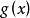



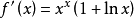
x | (0,1/e) | 1/e | (1/e,+∞) |
f '(x) | 負 | 0 | 正 |
f(x) | 單調減少 | 最小值 | 單調增加 |






x | (0,e) | e | (e,+∞) |
g'(x) | 正 | 0 | 負 |
g(x) | 單調增加 | 最大值 | 單調減少 |




