基本介紹
- 中文名:換底公式
- 外文名:base changing formula for logarithms
- 使用特點:尋找特殊值,換對對數
- 適用學科:數學、計算機編程、建築工程
- 適用範圍:對數的計算,高中數學
- 公式成立條件:對數的底均大於零且不等於1
簡單介紹
公式


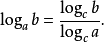
推導過程



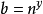




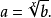










推論




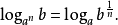



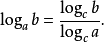



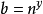




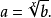














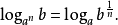
換底公式是高中數學常用對數運算公式,可將多異底對數式轉化為同底對數式,結合其他的對數運算公式一起使用。計算中常常會減少計算的難度,更迅速的解決高中範圍的對數...
對數公式是數學中的一種常見公式,如果a^x=N(a>0,且a≠1),則x叫做以a為底N的對數,記做x=log(a)(N),其中a要寫於log右下。其中a叫做對數的底,N叫做真...
019 對數的換底公式 020 平均增長率公式 數列 第2章 021 數列的通項an與前n項和Sn的關係式 022 數列的遞推公式 023 等差數列的定義式 024 等差數...
兩式相減得:利用換底公式, [1] 將ln換算成lg:阿倫尼烏斯公式指數形式 阿倫尼烏斯公式還可以引入一個指前因子(也稱頻率因子)A(preexponential factor)。...
,由指數函式換底公式得 。④、⑤、⑥如果根據導數的定義來推導的話就不能推廣到n為任意實數的一般情況,但 的導函式為 和y=lnx的導函式 ,根據複合函式的求導規...
性質8 對數換底公式推論1推論2推論3對數式例題解析 編輯 【例1】已知 ,求證明:由已知得 ,即 且 ,即因此 【例2】已知 求證證明:設已知比例式的比值為k,得...
1.換底公式 2.換底公式的套用 八、指數對數恆等式的證明及套用 1.證明指數對數恆等式 2.恆等式的套用 九、對數式大小的比較方法 1.利用單調性 2...
2.10 換底公式 2.11 對數函式及其性質 2.12 習題課4 小結 第三章 不等式 3.1 不等關係 3.2 不等式的解法 3.2.1 含有絕對值的不等式的解法 3.2.2 ...
性質二:log(a)(b)=1/log(b)(a) 證明如下: 由換底公式log(a)(b)=log(b)(b)/log(b)(a) ---取以b為底的對數log(b)(b)=1 =1/log(b)(a)...
③換元法 ④分解因式法 (4)對數方程的解法 ①定義法 ②換底公式法 ③比較真數法 ④換元法 5.數列問題的解法 (1)求數列通項公式的方法 ①觀察分析法 ②公...
如果ax=N(a>0,且a≠1),那么數x叫做以a為底N的對數,記作x=logaN,讀作...公式推導 運算性質 和差 換底公式 指系 還原 互換 倒數 鏈式 表達方式 與指數...
以10為底的對數,稱為常用對數。在高等數學中,常使用以e為底的對數,即自然對數。常用對數與自然對數可利用換底公式互換。對數不僅可用來簡化計算,而且在微積分、...
但是,也可以取其它對數底,採用其它相應的單位,它們間可用換底公式換算。最簡單的單符號信源僅取0和1兩個元素,即二元信源,其機率為P和Q=1-P,該信源的熵即...
①理解對數的概念及其運算性質,知道用換底公式能將一般對數轉化成自然對數或常用對數;通過閱讀材料,了解對數的產生歷史以及對簡化運算的作用。②通過具體實例,直觀了解...
然而,由對數的換底公式,logan和logbn只有一個常數因子不同,這個因子在大O記法中被丟棄。因此記作O(logn),而不論對數的底是多少,是對數時間算法的標準記法。...
利用換底公式可得一般形式為a>1時,Y隨X增大而增大,先快後慢;0<a<1時,Y隨X增大而減少,先快後慢。當以Y和lnX繪製的散點圖呈直線趨勢時,可考慮採用對數...
求根公式 韋達定理 高次方程 分式方程 有理方程 無理方程微分方程 分數指數 同次根式 異次根式 最簡根式 同類根式換底公式 反對數表 坐標平面 坐標原點 比例...
兩式相減得:利用換底公式, ,將ln換算成lg得:阿累尼烏斯方程指數形式 阿倫尼烏斯公式還可以引入一個指前因子A(preexponential factor,也稱頻率因子)。...
利用換底公式, 將ln換算成lg:阿瑞尼斯方程式指數形式 阿尼瑞斯公式還可以引入一個指前因子(也稱頻率因子)A(preexponential factor)。...
