對數式(logarithmic expression)是一類特殊的解析式,指含有對未知數進行對數運算的解析式,如log2(x2-1),logax+b都是關於x的對數式,簡稱對數式。
基本介紹
- 中文名:對數式
- 外文名:logarithmic expression
- 所屬學科:數學
- 所屬問題:初等代數(對數)
- 簡介:有對未知數進行對數運算的解析式
基本概念
相關性質
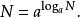


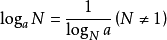

例題解析
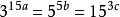


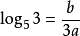














對數式(logarithmic expression)是一類特殊的解析式,指含有對未知數進行對數運算的解析式,如log2(x2-1),logax+b都是關於x的對數式,簡稱對數式。
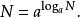


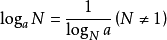

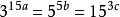


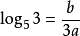













對數公式是數學中的一種常見公式,如果a^x=N(a>0,且a≠1),則x叫做以a為底N的對數,記做x=log(a)(N),其中a要寫於log右下。其中a叫做對數的底,N叫做真...
對數式(logarithmic expression)是一類特殊的解析式,指含有對未知數進行對數運算的解析式,如log2(x2-1),logax+b都是關於x的對數式,簡稱對數式。...
一般地,對數函式以冪(真數)為自變數,指數為因變數,底數為常量的函式。對數函式是6類基本初等函式之一。其中對數的定義:如果ax=N(a>0,且a≠1),那么數x...
在數學中,對數是對求冪的逆運算,正如除法是乘法的倒數,反之亦然。 這意味著一個數字的對數是必須產生另一個固定數字(基數)的指數。 在簡單的情況下,乘數中的...
如果a(a>0,且a≠1)的b次冪等於N,即ab=N,那么數b叫做以a為底N的對數,記作logaN=b(其中a叫做對數的底數,N叫做真數),這就是對數變換。...
對數方程(logarithmic equation)一種超越方程,指含有關於未知數的對數式,而不含其他超越式的方程。即在對數符號後面含有未知數的方程,叫做對數方程。...
對數視力表自1958年推出後,引起國內廣大眼科工作者的重視和肯定,其主要觀點是:“統計學裡要求同質才可相比。在五分法中用以測量視力的有視標、手指、手掌和光亮...
對數坐標指的是在二維直角坐標系下對數圖像對應的各點所處的位置,x稱為點A的橫坐標,y稱為點A的縱坐標。若一個數x(x>0)經過一個對數函式作用後變為y,如:...
對數線性模型描述的是機率與協變數之間的關係;對數線性模型也用來描述期望頻數與協變數之間的關係。...
換底公式是高中數學常用對數運算公式,可將多異底對數式轉化為同底對數式,結合其他的對數運算公式一起使用。計算中常常會減少計算的難度,更迅速的解決高中範圍的對數...
017 指數式與對數式的互化公式 018 對數的運算法則 019 對數的換底公式 020 平均增長率公式 數列 第2章 021 數列的通項an與前n項和Sn的關係式 022...
脈衝回聲式是指發射短脈衝超聲,脈衝重複頻率500~1000Hz,或者更高。接收放大,因體內回聲的振幅差別在100~120dB(105~10f)間,除高速數位化技術外,一般必須使用對數...
