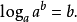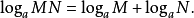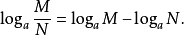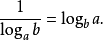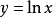背景 約翰·納皮爾/約翰·奈皮爾(John Napier,1550~1617),蘇格蘭數學家、神學家,對數的發明者。 Napier出身貴族,於1550年在蘇格蘭愛丁堡附近的小鎮梅奇斯頓(Merchiston Castle,Edinburgh,Scotland)出生,是Merchiston城堡的第八代地主,未曾有過正式的職業。 年輕時正值歐洲掀起宗教革命,他行旅其間,頗有感觸。蘇格蘭轉向新教,他也成了寫文章攻擊舊教(天主教)的急先鋒(主要文章於1593年寫成)。其時傳出天主教的西班牙要派無敵艦隊來攻打,Napier就研究兵器(包括拏炮、裝甲馬車、潛水艇等)準備與其拚命。雖然Napier的兵器還沒製成,英國已把無敵艦隊擊垮,他還是成了英雄人物。 他一生研究數學,以發明對數運算而著稱。那時候天文學家Tycho Brahe(第谷,1546~1601)等人做了很多的觀察,需要很多的計算,而且要算幾個數的連乘,因此苦不堪言。1594年,他為了尋求一種球面三角計算的簡便方法,運用了獨特的方法構造出對數方法。這讓他在數學史上被重重地記上一筆,然而完成此對數卻整整花了他20年的工夫。1614年6月在愛丁堡出版的第一本對數專著《奇妙的對數表的描述》("Mirifici logarithmorum canonis descriptio")中闡明了對數原理,後人稱為納皮爾對數:Nap logX。1616年Briggs(亨利·布里格斯,1561 - 1630)去拜訪納皮爾,建議將對數改良一下以十為基底的對數表最為方便,這也就是後來常用的對數了。可惜納皮爾隔年於1617年春天去世,後來就由Briggs以畢生精力繼承納皮爾的未竟事業,以10為底列出一個很詳細的對數表。並且於1619年發表了《奇妙對數規則的結構》,於書中詳細闡述了對數計算和造對表的方法。納皮爾對數字計算特別有研究,他的興趣在於球面三角學的運算,而球面三角學乃因應天文學的活動而興起的。他重新建立了用於解球面直角三角形的10個公式的巧妙記法——圓的部分法則(“納皮爾圓部法則”)和解球面非直角三角形的兩個公式——“納皮爾比擬式”,以及做乘除法用的“納皮爾算籌”。此外,他還發明了納皮爾尺,這種尺子可以機械地進行數的乘除運算和求數的平方根。
定義 若一個數x(x>0)經過一個
對數函式 作用後變為y,如:
,那么由x和y組成的二維向量
在二維坐標系下對應的點的
集合 ,就稱為一個點
的對數坐標。在二維
直角坐標系 下,x稱為點A的橫坐標,y稱為點A的
縱坐標 。
函式圖象 對於以a為底的對數函式, ①當0<a<1時,圖象上函式顯示為(0,+∞)單減。隨著a 的增大,圖象逐漸以(1,0)點為軸順時針轉動,但不超過X=1。②當a>1時,圖象上顯示函式為(0,+∞)單增,隨著a的增大,圖象逐漸以(1.0)點為軸逆時針轉動,但不超過X=1.
與其他函式與
反函式 之間圖象關係相同,對數函式和
指數函式 的圖象關於直線y=x對稱。
圖1.對數坐標示意圖 性質 坐標轉化 轉化原理 兩者間的轉化只相當於做一個函式變換,比如將y=f(x)的畫在縱軸為
對數 坐標的坐標圖上,跟經過
變換的z-x線性坐標上的圖形狀一樣。特別注意的是在各自
坐標軸 上的是
真數 ,不是求對數後的值。
例子 天狼50 的K線圖採用的是
對數 坐標系 ,縱向長度和股價漲幅的對數成
正比 。在普通坐標系中,所有當日漲跌金額相等的股票,其 K 線長度是一樣的,比如所有自開盤至收盤上漲 1 元錢的 K 線具有同樣的長度。可是,10元的股票漲1元和20元的股票漲1元,其上漲的幅度是不一樣的,在對數坐標系中,只有當日漲跌幅( % )相等的 股票,其K 線才具有同樣的長度,例如:所有自開盤至收盤上漲 10% 的股票,它們的 K 線在對數坐標中長度是一樣的。對於一隻股票而言,使用對數坐標系能夠更真實地反映股價的上漲和下跌幅度。
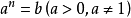

 圖1.對數坐標示意圖
圖1.對數坐標示意圖