簡介
波德圖是由
貝爾實驗室的荷蘭裔科學家亨德里克·韋德·波德在1930年發明。波德用簡單但準確的方法繪製增益及相位的圖,因此他發明的圖也就稱為波德圖。
波德圖幅頻圖的頻率用對數尺度表示,增益部分一般都用
功率的
分貝值來表示,也就是將增益取對數後再乘以20。由於增益用對數來表示,因此一傳遞函式乘以一常數,在波德增益圖只需將圖形的縱向移動即可,二傳遞函式的相乘,在波德幅頻圖就變成圖形的相加。幅頻圖縱軸0分貝以下具有正增益裕度、屬穩定區,反之屬不穩定區:
波德圖相頻圖的頻率也用對數尺度表示,而相位部分的單位一般會使用
度。配合波德相頻圖可以估算一信號進入系統後,輸出信號及原始信號的比例關係及
相位。例如一個
Asin(ω
t) 的信號進入系統後振幅變原來的
k倍,相位落後原信號Φ,則其輸出信號則為(
Ak)sin(ω
t−Φ),其中的
k和Φ都是
頻率的函式。相頻圖縱軸-180度以上具有正相位裕度、屬穩定區,反之屬不穩定區
若將系統的增益以
複數表示,則複數增益取對數後的虛部即為相位,因此二傳遞函式的相乘,在波德相點陣圖上也是圖形的相加。
波德圖的增益和相位很難單獨的變動、二者會互相牽扯,當調整系統的增益回響時,系統的相位回響也會隨之變化,反之亦然。最小相位系統的增益和相位特性之間可以用
希爾伯特轉換來轉換,因此知道其中一項即可求出另外一項。
若轉換函式是
有理函式,其零點及極點均為實數,則其波德圖可以用幾條漸近線的直線來近似,利用簡單的規則即可以徒手繪製。若近似的波德圖再修正每個
截止頻率時的增益值,則其近似值會更接近實際值。
波德圖手繪的規則
波德圖的前提就是可以處理以下型式函式的對數值:
上述函式的對數值可以轉換為極點及零點對數的和:
在繪製波德相點陣圖時直接使用了上述的概念。增益圖的繪製時則是以此概念為基礎,因為每個極點或零點其增益的對數均從0開始,而且其漸近線只有一個轉折點,因此繪製時可以再作簡化。
直線近似的增益圖
波德圖增益分貝值一般都利用 20log10(X)的公式。考慮以下的轉換函式:
其中
及
是常數,s=jΩ,a
n,b
n>0,而
H是轉換函式。
在每個對應{\displaystyle \omega =x_{n}}(零點)的位置,將直線的斜率增加{\displaystyle 20\cdot a_{n}\ dB}/十倍頻。
在每個對應{\displaystyle \omega =y_{n}}(極點)的位置,將直線的斜率減少{\displaystyle 20\cdot b_{n}\ dB}/十倍頻。
圖在起始點時的增益值,可以依照圖中的角頻率下限,計算其對應的|H(jω)|。
圖在起始點時的斜率則依照有多少零點及極點低於角頻率下限,再依上述二個方式計算斜率,若所有點及極點均高於角頻率下限,起始點時的斜率為零。
在處理無法分解的二次多項式{\displaystyle ax^{2}+bx+c\ }時,多半可以用{\displaystyle ({\sqrt {a}}x+{\sqrt {c}})^{2}}的方式近似。
波德圖(Bode)是振動的幅值(尤指工頻分量或二階分量)和相位隨轉速而變化的圖。與頻響函式的幅、相頻特性曲線類似。從波德圖上可以清楚的看出轉子過臨界轉速的振動狀況。
波德圖(bode)是反映機器振動幅值、相位隨轉速變化的關係曲線。圖形的橫坐標是轉速,縱坐標有兩個,一個是振幅的峰-峰值,另一個是相位。從波德圖上我們可以得到以下信息:
 波德圖
波德圖a. 轉子系統在各種轉速下的振幅和相位;
b. 轉子系統的臨界轉速;
c. 轉子系統的共振放大係數(Q=Amax/ε);一般小型機組Q在3~5甚
至更小,而大型機組在5~7;超過上述數值,很可能是不安全的;
d. 轉子的振型;
e. 系統的阻尼大小;
f. 轉子上機械偏差和電氣偏差的大小;
g. 轉子是否發生了熱彎曲。
穩定性
一般是指作用在系統上的擾動排除後,系統能否恢復原狀、或以怎樣的精度恢復原狀的性能。它是控制理論的一個極其重要的問題。在經典控制理論中,一般涉及到的是定常的線性系統,有關這種系統的穩定性的判別方法主要有: 羅斯—胡爾維茨準則、奈奎斯特判據、波德圖、尼柯爾圖和
根軌跡法等。在現代控制理論中,對線性系統和非線性系統的穩定性的研究,主要是李雅普諾夫的穩定性理論。
李雅普諾夫根據系統的輸出 (回響) 是否有界來定義系統的穩定性,並區分了三種情況: (1) 穩定的,即對於系統初始值的一個擾動,如果其回響的幅值是有界的。(2) 漸近穩定的,即對於系統初始值的一個擾動,如果其回響能夠最終回到初始狀態。(3)不穩定的,即對於系統初始值的一個擾動,其回響的幅值不是有界的。經典控制理論所研究的穩定性只限於第二種情況漸近穩定,而把另兩種情況都看作是不穩定的。因而李雅普諾夫的穩定性概念更具一般性。李雅普諾夫用兩種方法分析系統的穩定性,第一種方法是: 用近似極數表示非線性函式,然後用近似方法求解非線性方程,最後根據解的性質,確定其系統的穩定性; 第二種方法是: 不必求解方程,而用李雅普諾夫函式的純量函式來判別系統是否穩定,並分析系統的回響。由於第二種方法具有不必求解方程的特點,因而也稱直接法,而稱第一種方法為間接法。由於許多非線性系統和時變系統的方程是難以求解的,又由於通過計算機可以找到所需的李雅普諾夫函式,還能找到系統的穩定區域,所以第二種方法在控制理論中得到廣泛套用。穩定性對於社會經濟系統極為重要,是經濟學經常討論的重要課題之一。探討經濟系統的穩定性,對於了解經濟系統的動態發展規律、預測經濟發展方向以及分析經濟系統的結構等,都有著重要的現實意義。

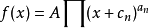
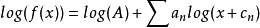
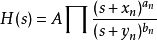

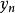
 波德圖
波德圖