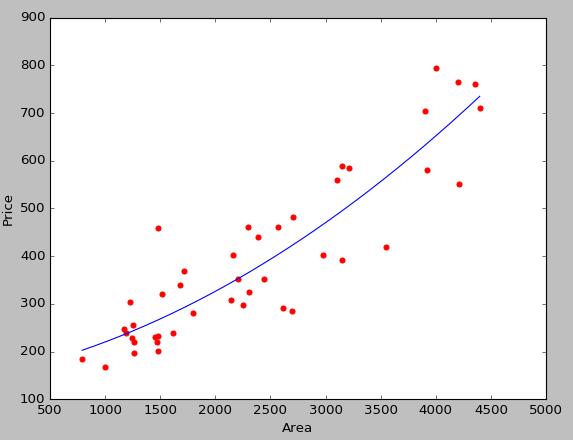
多項式回歸，回歸函式是回歸變數多項式的回歸。多項式回歸模型是線性回歸模型的一種，此時回歸函式關於回歸係數是線性的。由於任一函式都可以用多項式逼近，因此多項式回歸有著廣泛套用。
基本介紹
- 中文名：多項式回歸
- 外文名：Polynomial Regression
- 所屬學科：數理科學
- 類型：計算機科學
- 學科：跨學科
- 性質：回歸
- 概念：研究多項式的回歸分析
介紹,多項式回歸分析,套用,
介紹
直線回歸研究的是一個因變數與一個自變數之間的回歸問題，但是，在畜禽、水產科學領域的許多實際問題中，影響因變數的自變數往往不止一個，而是多個，比如綿羊的產毛量這一變數同時受到綿羊體重、胸圍、體長等多個變數的影響，因此需要進行一個因變數與多個自變數間的回歸分析，即多元回歸分析。
研究一個因變數與一個或多個自變數間多項式的回歸分析方法，稱為多項式回歸（Polynomial Regression）。如果自變數只有一個時，稱為一元多項式回歸；如果自變數有多個時，稱為多元多項式回歸。在一元回歸分析中，如果變數y與自變數x的關係為非線性的，但是又找不到適當的函式曲線來擬合，則可以採用一元多項式回歸。
一元m次多項式回歸方程為：
。
二元二次多項式回歸方程為：
。
多項式回歸的最大優點就是可以通過增加x的高次項對實測點進行逼近，直至滿意為止。事實上，多項式回歸可以處理相當一類非線性問題，它在回歸分析中占有重要的地位，因為任一函式都可以分段用多項式來逼近。因此，在通常的實際問題中，不論依變數與其他自變數的關係如何，我們總可以用多項式回歸來進行分析。
多項式回歸分析
多項式回歸問題可以通過變數轉換化為多元線性回歸問題來解決。
因此用多元線性函式的回歸方法就可解決多項式回歸問題。需要指出的是，在多項式回歸分析中，檢驗回歸係數
是否顯著，實質上就是判斷自變數x的i次方項對因變數y的影響是否顯著。
模型如以下形式的稱為一元多項式回歸模型：
套用
多項式回歸在回歸分析中很重要，因為任意一個函式至少在一個較小的範圍內都可以用多項式任意逼近，因此在比較複雜的實際問題中，有時不問y與諸元素的確切關係如何，而用回歸分析進行分析運算。
比如，對房屋成交信息建立多項式回歸方程，並依據回歸方程對房屋價格進行預測 。
實例數據：如圖1，為了方便展示，成交信息只使用了房屋的面積以及對應的成交價格。
圖1
實驗過程：使用算法為線性回歸
實現步驟：
1、建立工程並導入sklearn包
import matplotlib.pyplot as pltimport numpy as npfrom sklearn import linear_modelfrom sklearn.preprocessing import PolynomialFeatures
2、載入訓練數據，建立回歸方程
# 讀取數據集datasets_X = []datasets_Y = []fr = open('prices.txt','r')lines = fr.readlines()for line in lines: items = line.strip().split(',') datasets_X.append(int(items[0])) datasets_Y.append(int(items[1]))length = len(datasets_X)datasets_X = np.array(datasets_X).reshape([length,1])datasets_Y = np.array(datasets_Y)minX = min(datasets_X)maxX = max(datasets_X)X = np.arange(minX,maxX).reshape([-1,1])poly_reg = PolynomialFeatures(degree = 2)X_poly = poly_reg.fit_transform(datasets_X)lin_reg_2 = linear_model.LinearRegression()lin_reg_2.fit(X_poly, datasets_Y)
3、可視化處理
# 圖像中顯示plt.scatter(datasets_X, datasets_Y, color = 'red')plt.plot(X, lin_reg_2.predict(poly_reg.fit_transform(X)), color = 'blue')plt.xlabel('Area')plt.ylabel('Price')plt.show()
實驗結果：通過多項式回歸擬合的曲線與數據點的關係如圖2所示。依據該多項式回歸方程即可通過房屋的尺寸，來預測房屋的成交價格。
圖2
