域上代數相關集(algebraically dependent setover a field)是與超越基密切相關的一個概念。設K是F的域擴張,S是K的子集。若y∈K是F(S)上的代數元,則稱y在F上與S是代數相關的;否則,稱為代數無關的。
基本介紹
- 中文名:域上代數相關集
- 外文名:algebraically dependent setover a field
- 領域:數學
- 學科:域論
- 性質:與超越基密切相關的概念
概念
超越基
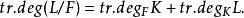
域上代數相關集(algebraically dependent setover a field)是與超越基密切相關的一個概念。設K是F的域擴張,S是K的子集。若y∈K是F(S)上的代數元,則稱y在F上與S是代數相關的;否則,稱為代數無關的。
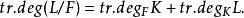
《有限域上代數函式域及編碼套用》是依託華東師範大學,由楊思熳擔任項目負責人的青年科學基金項目。項目摘要 有限域上代數曲線的數論性質一直是代數幾何,代數數論及其相關領域的一個重要課題,許多知名數學家(如A. Weil, J. P. Serre...
《有限域上代數簇的指數和與L-函式及其套用》是依託寧波大學,由曹煒擔任負責人的國家自然科學基金資助面上項目。項目簡介 代數簇上的有理點問題是丟番圖方程的中心問題. 而有限域上代數簇的有理點個數可以通過指數和表示出來,從而將...
循環代數(cyclic algebras)是特殊的有限中心單代數。一個有限中心單代數A,若它有嚴格極大子域E,使得E/F是循環擴張,則稱A為循環代數。代數數域上的有限中心可除代數是循環代數,有理數域上的每個單代數都是其中心上的循環代數。這...
《有限域上代數簇的指數和》是依託上海交通大學,由劉春雷擔任項目負責人的面上項目。項目摘要 本項目研究有限域上的代數簇的指數和,包括p-階、p的方冪階指數和及T-進指數和。對p的方冪階指數和,我們研究其L-函式的p-進牛頓...
一方面,對於複數域上的不規則代數簇,我們將藉助典範層或者多典範層的Fourier-Mukai變換以及上同調支集來研究它們的多典範映射和幾何結構,擬得到一個下界N使得N-典範映射和Iitaka纖維化一致,並刻畫一類歐拉特徵為零的代數簇。另一方面,...
二次代數函式域,明顯決定了幾類實二次函式域的基本單位,決定了多類二次函式域的理想類數的下界,給出了類數為 1 的條件,給出了理想類群的結構的一系列定理。發展套用了函式連分式理論。概念 一個域上的 n(n≥1) 元有理函式...
§3分裂域上不可約常表示的個數 §4特徵標表計算舉例 §5從特徵標表讀群的結構 §6整性定理與不可約復表示的維數 §7Burnside可解性定理 第3章 代數的表示 §1域上代數 §2代數上的模範疇 §3Jordan-HSlder定理 §4Wedderl...
對代數數論、代數幾何和算術代數幾何有基本的重要貢獻。工作包括shafarevich-weil定理,golod-shafarevich定理、tate-shafarevich群、 grothendieck-ogg-shafarevich公式、néron-ogg-shafarevich 準則、有限可解群是有理數域上的galois群的證明、...
則它們組成R上代數 Q 的一個基,而 Q 關於此基的乘法表是:1是單位元。這就是著名的四元數代數。實數域 由於推廣數系而得出四元數代數,隨之產生出實數域與複數域上的結合代數的概念,最初曾稱之為:“超複數系”。實數域上有限...
