設0≤X1≤X2≤…≤Xn≤…是一單調非負隨機變數列。那么,若Xn(處處)收斂於隨機變數X,則相應的數學期望列EX1,EX2,…,EXn,…收斂於X的數學期望EX,這種現象稱為單調收斂定理。
基本介紹
- 中文名:單調收斂定理
- 外文名:Monotone convergence theorem
- 類別:數學
- 推廣:勒貝格單調收斂定理
- 收斂:有限有界的
- 套用:高等函式求極限
單調實數序列的收斂性
定理
證明








單調級數的收斂性定理

勒貝格單調收斂定理
定理
證明








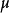

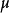
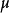




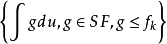






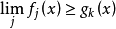
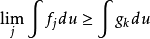


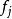











設0≤X1≤X2≤…≤Xn≤…是一單調非負隨機變數列。那么,若Xn(處處)收斂於隨機變數X,則相應的數學期望列EX1,EX2,…,EXn,…收斂於X的數學期望EX,這種現象稱為單調收斂定理。

















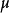

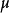
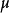




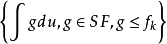






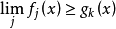
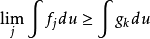


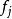










設0≤X1≤X2≤…≤Xn≤…是一單調非負隨機變數列。那么,若Xn(處處)收斂於隨機變數X,則相應的數學期望列EX1,EX2,…,EXn,…收斂於X的數學期望EX,這種現象稱...
對一般的條件收斂級數,也可以用以上的算法來證明黎曼級數定理。上文中有關交錯調和級數的算法之所以成立,原因有二:首先,所有正項構成的級數發散到正無窮大,所有負...
實數連續性定理包括:確界存在性定理,單調有界收斂定理,閉區間套定理,有限覆蓋定理,聚點定理,波爾查諾——魏爾斯特拉斯定理、柯西準則。 這七個定理可由確界存在...
其中函式極限是在逐點收斂的意義上的極限,函式取值和積分可以是無窮大。法圖引理驗證推導 編輯 定理證明基於單調收斂定理。設 為函式列的下極限。對每一個正整數 ...
收斂的充要條件是:數列{xn} 的任何非平凡子列都收斂。 lim單調收斂定理 單調有界數列必收斂 lim函式極限 編輯 設函式 在點 的某一去心鄰域內有定義,如果存...
但這裡有一個很微妙的問題,即與完備性公理等價的7個實數系的基本定理(確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和柯西收斂...
第4章 積分極限定理4.1 單調收斂定理4.2 Fatou引理4.3 Lebesgue控制收斂定理第5章 可測函式與可測集5.1 階梯函式和正則函式5.2 可測函式的概念和運算5.3 可...
存在,根據單調收斂定理可知序列 是收斂的;採樣機制(它有效地避免了窮舉)和各種狀態轉變運算元的交替使用可以很好的節省搜尋時間; 狀態轉移中對變換因子的調整可以控制...
2.1.2 單調收斂定理2.1.3 Lebesgue積分的基本性質2.2 積分收斂定理及套用2.2.1 積分收斂定理2.2.2 Riemann可積性2.2.3 可測函式的連續性...
4.2 單調收斂定理4.3 一般可測函式的Lebesgue積分與可積函式空間4.4 控制收斂定理4.5 Lebesgue積分與Riemann積分的關係4.6 可積函式與連續函式的關係4.7 分布與積分...
4.2 單調收斂定理4.3 一般可測函式的lebesgue積分與可積函式空間4.4 控制收斂定理4.5 lebes詞條標籤: 出版物 , 書籍 圖集 測度與積分圖冊 V百科往期回顧 詞條...
控制收斂定理:幾乎處處有界的r.v.序列,如果有極限,那么期望與極限可以交換。 有上面兩個定理,我們就可以給出線性平穩序列的各種性質了! 即非負單調遞增r.v.序列...
類似地,單調收斂定理,聚點原理等也可用作連續性公理。公理組II也有其他提法。用公理定義了實數系R後,可以繼續定義 R 的特殊元素正整數、整數等。例如,由數1生成...
8.2 一維情形:比較定理與半群 8.3 BSDE的單調收斂定理 8.4 定價系與夕期望 8.5 g鞅與非線性Doob-Meyer分解定理 8.6 F期望與F鞅 8.7 反比較定理及其套用 8.8...
