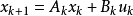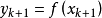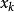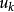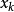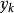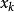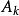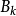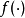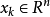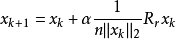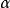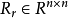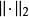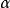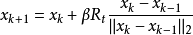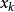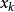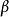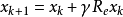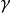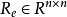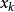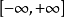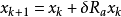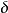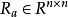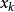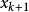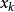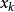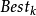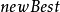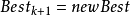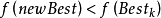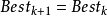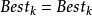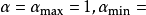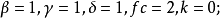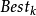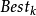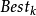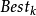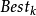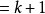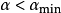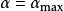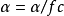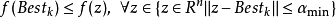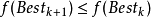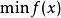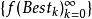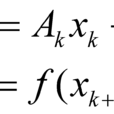基本介紹
- 中文名：狀態轉移算法
- 外文名：State transition algorithm (STA)
統一框架,一種連續狀態轉移算法,狀態轉換運算元,鄰域和採樣,更新策略,基本連續狀態轉移算法的流程,基本連續狀態轉移算法背後的原理,其它相關連結,
統一框架
狀態轉移算法用狀態空間表達式來統一描述產生候選解的統一框架：
其中，
作為一種全局最佳化算法，在設計狀態轉移算法時，使其具備以下性質：
- 全局性，狀態轉移算法具有在整個空間進行搜尋的能力；
- 最優性，狀態轉移算法可以保證找到一個最優解；
- 收斂性，通過狀態轉移算法產生的解序列是收斂的；
- 快速性，狀態轉移算法儘可能地節省搜尋時間；
- 可控性，狀態轉移算法可以控制搜尋空間的幾何形態。
一種連續狀態轉移算法
在連續狀態轉移算法中，
是一個連續變數，設計了四個特殊的狀態轉換運算元來產生新的候選解。
狀態轉換運算元
(1) 旋轉變換（Rotation Transformation, RT）
這裡
是一個正常數，稱作旋轉因子，
是一個隨機矩陣，它裡面的每個元素服從[-1,1]的均勻分布，
表示向量的二範數。旋轉變換具有在半徑為 的超球體內搜尋的功能。
(2)平移變換（Translation Transformation, TT）
這裡
是一個正常數，稱作平移因子，
是一個服從[0,1]均勻分布的隨機變數。平移變換具有沿著從點
到點
直線上並以 為起點最大長度為 進行線搜尋的功能。
(3)伸縮變換（Expansion Transformation, ET）
這裡
是一個正常數，稱作伸縮因子，
是一個隨機對角矩陣，它裡面的每個元素服從高斯分布。伸縮變換具有使 中的每個元素伸縮變換到
的功能，從而實現在整個空間進行搜尋。
(4)坐標搜尋（Axesion Transformation, AT）
這裡
是一個正常數，稱作坐標因子，
是一個隨機對角稀疏矩陣，它只在某個隨機位置有非零元素，且該元素服從高斯分布。坐標搜尋具有沿著坐標軸方向搜尋的功能，它的目的是為了增強單維搜尋能力。
鄰域和採樣
對於一個給定的當前狀態 ，下一個狀態
是通過上面介紹的狀態變換運算元產生的。考慮到狀態轉移矩陣的隨機性，可知產生的候選解不是唯一的。不難想像，對於給定的 ，當利用某種狀態變換運算元時，產生的所有候選解將自動形成一個鄰域。
對於給定的 ，考慮到狀態轉移矩陣中的元素服從某種隨機分布，產生的候選解是一個隨機向量，它對應的特定值可以看成一個樣本。此外，對於某種狀態變換運算元和給定當前狀態，考慮到其對應的狀態轉移矩陣的產生是獨立的，當獨立運行多次後，比如獨立運行SE次後，將會產生SE個樣本。
更新策略
在給定當前最好解
的基礎上，對於某種狀態變換運算元，利用上面闡述的採樣策略，將會產生SE個候選解。記SE個候選解中的最好解為
，則通過如下的策略來更新當前最好解
基本連續狀態轉移算法的流程
基本連續狀態轉移算法由上面介紹的狀態變換運算元，採樣機制與更新策略融合而成，其算法的流程如下：
Step 1：隨機產生一個初始解
，設定算法參數
1e-4,
Step 2: 基於當前最好解 ，利用伸縮變換操作產生SE個樣本，並利用更新策略更新當前最好解，如果當前最好解有變動，執行平移變換操作並以同樣的機制更新當前最好解 。
Step 3: 基於當前最好解 ，利用旋轉變換操作產生SE個樣本，並利用更新策略更新當前最好解，如果當前最好解有變動，執行平移變換操作並以同樣的機制更新當前最好解 。
Step 4: 基於當前最好解 ，利用坐標搜尋操作產生SE個樣本，並利用更新策略更新當前最好解，如果當前最好解有變動，執行平移變換操作並以同樣的機制更新當前最好解 。
Step 5: 置
，如果
，置
，否則置
，然後重返Step2直到終止條件滿足。
基本連續狀態轉移算法背後的原理
- 伸縮變換運算元具有在整個空間進行搜尋的能力，使其滿足全局性；
- 旋轉變換運算元中，當旋轉因子充分小時，當前的最好解將變成一個局部最優解，即；
- 更新策略可以保證狀態轉移算法的收斂性，因為
且假定
存在，根據單調收斂定理可知序列
是收斂的；
- 採樣機制(它有效地避免了窮舉)和各種狀態轉變運算元的交替使用可以很好的節省搜尋時間;
- 狀態轉移中對變換因子的調整可以控制搜尋空間的幾何形態。
其它相關連結
狀態轉移算法的MATLAB程式
