基本介紹
- 中文名:單純多面體
- 外文名:simplicial polytope
- 適用範圍:數理科學
簡介
單純形
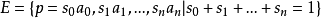

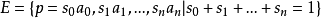
單純多面體是由一類多面體派生的另一類多面體,指除多面體P自身及空集外,P的所有面均為單純形的多面體。...
r單純多面體(r-simplicial polytope)一類特殊的單純多面體.所有:維面為單純形的多面體,這裡1鎮r鎮d-l,d為多面體的維數. ...
單純形是代數拓撲中最基本的概念。單純形是三角形和四面體的一種泛化,一個k維單純形是指包含 k+1個節點的凸多面體。...
退化多面體,是一類特殊的多面體。在數學中,退化的情況是一種極限情況,其中一類對象的一個元素在質量上與其餘的類不同,因此屬於另一個通常較簡單的類。許多複合或...
單純映射(simplicial map)是聯繫復形的多面體之間的一類重要映射。它是從復形K的多面體|K|到復形L的多面體|L|的連續映射,任何連續映射在某種意義下可用它逼近,可...
單純逼近是與連續映射相關的單純映射。需要注意,並不是任何兩個復形的多面體之間的連續映射都存在單純逼近。...
單純同調序列(simplicial homology sequence)是同調群所具有的一種性質。復形偶(K,L)與K和L的各種同調關係表現為它們的同調群組成的一個正合的序列,即單純同調...
單純鏈映射(simplicial chain map)是由單純映射決定的鏈映射。鏈映射是聯繫復形的鏈群之間的一種系列同態。為了使復形的鏈群之間的同態能誘導出同調群之間的同態,...
單純形加速(simplex acceleration)是單純形法的推廣,指單純形法中的擴展、壓縮、縮邊。是由Spendley等三人於1962年提出,並在1964年經Nelder等兩人加以改進的,為了...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。單純同調群是一個重要的拓撲不變數,它也是同倫型不變數。復形K的鏈...
在幾何學中,三面體(英文:Trihedron)是指由3個面組成的多面體。面為平面的三面體在三維空間不能存在,因為要至少四個頂點才能在三維空間形成有體積的多面體,除非它...
前面討論的單水平的單純形最佳化法,可以用來確定最佳的試驗條件,但不能判斷各因素對回響值影響的相對大小,然而,從實際工作的觀點來看,了解各因素對回響值影響的相對...
