單純形加速(simplex acceleration)是單純形法的推廣,指單純形法中的擴展、壓縮、縮邊。是由Spendley等三人於1962年提出,並在1964年經Nelder等兩人加以改進的,為了避免與求解線性規劃問題套用較成熟的單純形法區別,有人建議稱之為可變多面體法。
基本介紹
- 中文名:單純形加速
- 外文名:simplex acceleration
- 所屬學科:數學
- 簡介:單純形法中的擴展、壓縮、縮邊
- 別稱:可變多面體法
基本介紹
 圖1(a)
圖1(a) 圖2
圖2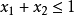

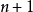
舉例說明
























單純形加速(simplex acceleration)是單純形法的推廣,指單純形法中的擴展、壓縮、縮邊。是由Spendley等三人於1962年提出,並在1964年經Nelder等兩人加以改進的,為了避免與求解線性規劃問題套用較成熟的單純形法區別,有人建議稱之為可變多面體法。
 圖1(a)
圖1(a) 圖2
圖2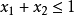

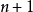























單純形加速(simplex acceleration)是單純形法的推廣,指單純形法中的擴展、壓縮、縮邊。是由Spendley等三人於1962年提出,並在1964年經Nelder等兩人加以改進的,為了...
單純形最佳化法simplex r>p}imiza}ion nx"}hnd簡稱單純形法。利用多維空間中的一種凸圖形(即單純形)移動實現實驗參數最佳化的一種動態凋優方法,每一次選用的試驗...
單純形搜尋法(Simplex search)由指導搜尋的簡單策略刻劃。第一個單純形方法是在...這些算法試圖利用在搜尋過程中獲得的函式曲率的信息構造方向來加速搜尋。...
屬於直接型的算法有交替方向法(又稱坐標輪換法)、模式搜尋法、旋轉方向法、鮑威爾共軛方向法和單純形加速法等。約束最最佳化方法指前述一般非線性規劃模型的求解方法...
屬於直接型的算法有交替方向法(又稱坐標輪換法)、模式搜尋法、旋轉方向法、鮑威爾共軛方向法和單純形加速法等。非線性規劃約束法 指前述一般非線性規劃模型的求解...
4.2.3單純形加速法 4.2.4最速下降法 4.2.5共軛梯度法 4.2.6變尺度法 4.3約束條件下的最佳化方法 4.3.1消元法 4.3.2拉格朗日(lagrangian)乘子法 4.3.3罰函式...
在調節時間上我們選擇外環時間T大於內環時間T的3倍,步長上我們選擇分段可變步長,PID參數的整定上我們選擇具有控制參數收斂快,計算工作量相對較小,實用的單純形加速...
