劉維爾函式(Liouville function)是重要的數論函式之一,設Ω(n)表示正整數n的全部素因子的個數(要計算重數),則數論函式λ(n)=(-1)Ω(n)稱為劉維爾函式。如λ(1)=1,λ(2)=-1,λ(3)=-1,λ(4)=1等。
基本介紹
- 中文名:劉維爾函式
- 外文名:Liouville function
- 所屬學科:數學
- 所屬問題:初等數論(數論函式)
- 提出者:劉維爾(J.Liouville)
定義
劉維爾函式的性質





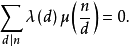
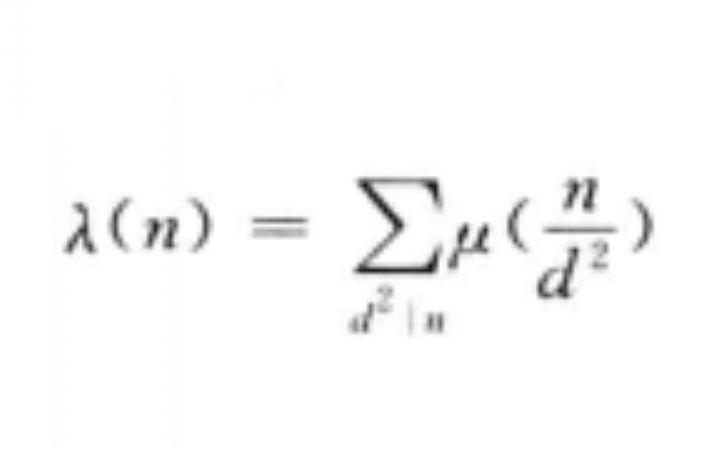
劉維爾函式(Liouville function)是重要的數論函式之一,設Ω(n)表示正整數n的全部素因子的個數(要計算重數),則數論函式λ(n)=(-1)Ω(n)稱為劉維爾函式。如λ(1)=1,λ(2)=-1,λ(3)=-1,λ(4)=1等。





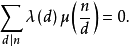
劉維爾函式(Liouville function)是重要的數論函式之一,設Ω(n)表示正整數n的全部素因子的個數(要計算重數),則數論函式λ(n)=(-1)Ω(n)稱為劉維爾函式。如...
在數學中,劉維爾方程(Liouville equation),又稱劉維 - 布拉-蓋爾芬德方程(Liouville-Bratu-Gelfand equation)是一個非線性特徵值泊松方程,以數學家約瑟夫·劉維爾(...
劉維爾公式是一個關於多重積分和歐拉積分的公式。...... 劉維爾公式是一個關於多重積分和歐拉積分的公式。中文名 劉維爾公式 外文名 Liouville's Formula 提出...
劉維爾(Joseph Liouville) 法國數學家,一生從事數學、力學和天文學的研究,涉足廣泛,成果豐富,尤其對雙周期橢圓函式、微分方程邊值問題和數論中的超越數問題有深入...
劉維爾(Liouville)定理是復變函式中的基本定理之一,其內容可簡單描述為“一個有界的整函式必是常函式"。注:整函式為在有限複平面上解析的復函式。...
施圖姆-劉維爾問題,即施圖姆-劉維爾理論,在數學及其套用中,以雅克·夏爾·弗朗索瓦·施圖姆(1803–1855)和約瑟夫·劉維爾(1809–1882)的名字命名,具體定義見正文。....
斯圖姆一劉維爾邊值問題(Sturm-Liouville bo-undary value problem)最基本而重要的一類微分方程特徵值問題.二階微分方程的特徵值問題。...
在數學中,黎曼-劉維爾積分是逐次不定積分的一種分數階推廣,以數學家波恩哈德·黎曼與約瑟夫·劉維爾命名。...
Gamma 函式從它誕生開始就被許多數學家進行研究,包括高斯、勒讓德、魏爾斯特拉斯、劉維爾等等。這個函式在現代數學分析中被深入研究,在機率論中也是無處不在,很多...
3.默比烏斯函式μ(n)的逆μ-1(n)=U(n)≡1。4.劉維爾函式λ(n)的逆λ-1(n)=μ(n)λ(n)。5.設g(n)=λ*U= ,則 [1] ...
對於Re(s)>1,ζ函式的對數由下式給出:其中 為馮·曼戈爾特函式。其導數由下式給出:更廣泛的性質如下:對於一個劉維爾函式, ,有:...
劉維爾(Joseph Liouville) 法國數學家,一生從事數學、力學和天文學的研究,涉足廣泛,成果豐富,尤其對雙周期橢圓函式、微分方程邊值問題和數論中的超越數問題有深入...
3.3.3 母函式關係3.3.4 正交的施圖姆-劉維爾多項式解集的完備性定理3.3.5 正交多項式解集在數值積分中的套用3.4 與多項式的施圖姆-劉維爾系統有關的方程和...
2.2.1 斯圖姆—劉維爾方程2.2.2 邊值條件和初始條件2.2.3 本徵值與本徵函式2.3 諧振問題2.3.1 諧振方程的通解2.3.2 諧振問題的本徵值及本徵函式...
因此﹐在天文學文獻中也稱為金斯方程或劉維爾方程。金斯對引力勢 V 作了一些理想的簡化假設﹐然後求解分布函式的通積分。從此開始了星系動力學的理論研究。...
