基本介紹
- 中文名:全等
- 外文名:Congruent
- 相關:全等三角形
- 基本解釋:兩個圖形形狀相同
- 學科:幾何數學
- 表示:≌
概念
釋義
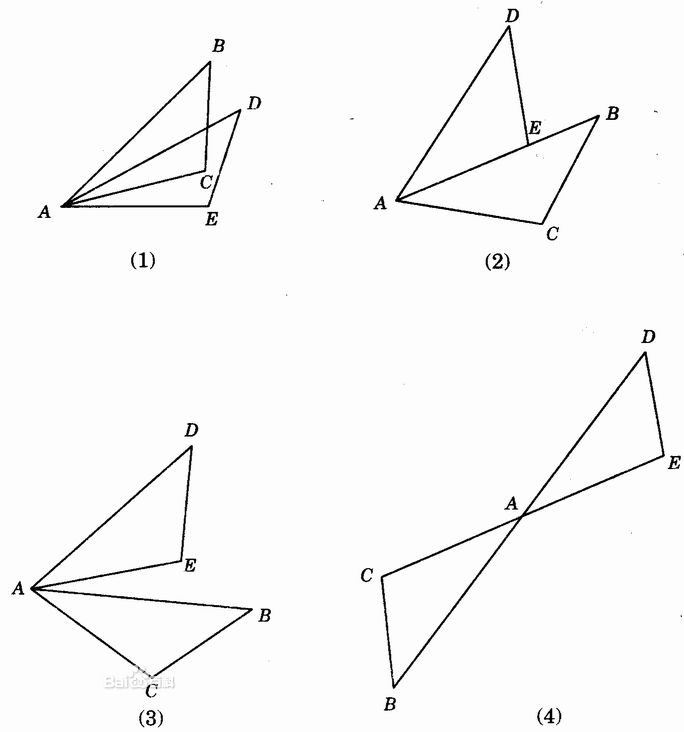 圖1 幾種全等示意圖
圖1 幾種全等示意圖
 圖1 幾種全等示意圖
圖1 幾種全等示意圖若兩個幾何圖形的形狀相同,則稱這兩個圖形是全等的圖形。全等是相似的一種特例。當相似比為1時,兩圖形全等。...
全等於“≌”表示兩個圖形能完全重合(包括形狀和面積)...... 全等於“≌”表示兩個圖形能完全重合(包括形狀和面積) 中文名 全等於 外文名 identically equal to...
全等形在通常的平面幾何里,把平面上的一個圖形搬到另一個圖形上,如果它們完全重合,那么這兩個圖形叫做全等圖形,簡稱全等形。...
經過翻轉、平移後,能夠完全重合的兩個三角形叫做全等三角形,而該兩個三角形的三條邊及三個角都對應相等。全等三角形指兩個全等的三角形,它們的三條邊及三個角...
在通常的平面幾何里,把平面上的一個圖形搬到另一個圖形上,如果它們完全重合,那么這兩個圖形叫做全等圖形,簡稱全等形。...
在平面幾何里,如果兩個圖形不僅形狀相同,而且大小也相等,能夠完全重合,則這兩個圖形為全等形。兩個全等形之間的關係稱為全等關係。...
AAS,即“角角邊”判定定理,一種非常實用的三角形全等證明方法。教科書中的解釋為:兩個角和其中一個角的對邊對應相等的兩個三角形全等。...
全等三角形是國中知識一個重點,考試時經常會以填空、選擇、解答題的形式出現,所占分值比例較大,所以學習全等三角形尤為重要。全等三角形共有5種判定方式:SSS、SAS...
在平面到自身的一一變換下,如果任意線段的長和它的象的長總相等,那么這種變換叫做全等變換,或稱契約變換。...
兩邊和它們的夾角對應相等的兩個三角形全等,簡寫成“邊角邊”或“SAS”.其中書寫中要注意是“夾邊”。...
全等溶解,dissolve congruently,是造岩礦物在地下水中進行成分一致的溶解。...... 全等溶解,dissolve congruently,是造岩礦物在地下水中進行成分一致的溶解。...
全等球面圖形(congruent spherical figures)兩球面圖形的一種等價關係...... 全等球面圖形(congruent spherical figures)兩球面圖形的一種等價關係 全等球面圖形(congruent...
如果將一個三角形平移、旋轉、翻折後能與另一個三角形全等,那么這兩個三角形叫做全等三角形。同樣,球面上的全等三角形也是這么定義的。...
數學上證明兩個三角形全等的一個定理:如果兩個直角三角形的斜邊和一條直角邊分別對應相等,那么這兩個直角三角形全等.(簡寫為:HL),其中:H是hypotenuse(斜邊)的...
一種可證明兩個三角形全等的方法...... 證明兩個三角形全等 假設存在兩個三角形ABC,DEF,若∠ABC=∠DEF,BC=EF,∠BCA=∠EFD,則三角形ABC≌三角形DEFV百科往期...
礦物與水接觸產生溶解反應時,其反應產物除溶解組分外,還有新生成的一種或多種礦物或非晶質固體成分,這種反應稱作非全等溶解(dissolve incongruently)。 ...
HL定理是證明兩個直角三角形全等的定理,通過證明兩個直角三角形直角邊和斜邊對應相等來證明兩個三角形全等。判定定理為:如果兩個直角三角形的斜邊和一條直角邊對應...
SSS,三組對應邊分別相等的兩個三角形全等(簡稱SSS或“邊邊邊”)。... 1、三組對應邊分別相等的兩個三角形全等(簡稱SSS或“邊邊邊”),這一條也說明了三角形具...
邊邊邊定理,簡稱SSS,是平面幾何中的重要定理之一。邊邊邊定理的內容是:有三邊對應相等的兩個三角形全等。它用於證明兩個三角形全等。該定理最早由歐幾里得證明。...
判定定理6:如果兩個三角形全等,那么這兩個三角形相似(相似比為1:1)(簡敘為:全等三角形相似)。相似的判定定理與全等三角形基本相等,因為全等三角形是特殊的相似...
三角分別相等,三邊成比例的兩個三角形叫做相似三角形(similar triangles)相似三角形是幾何中重要的證明模型之一,是全等三角形的推廣。全等三角形可以被理解為相似比...
正多面體,是指多面體的各個面都是全等的正多邊形,並且各個多面角都是全等的多面角。其中面數最少的是正四面體,面數最多的是正二十面體。有些化學物質的結晶體...
