依測度收斂(convergence in measure)是實變函式論中重要的收斂概念之一。
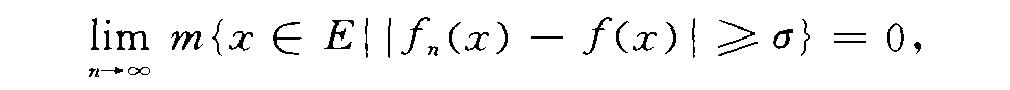
依測度收斂(convergence in measure)是實變函式論中重要的收斂概念之一。
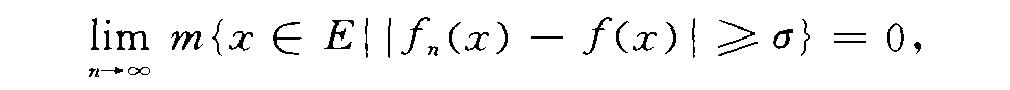
依測度收斂(convergence in measure)是實變函式論中重要的收斂概念之一。...... 依測度收斂(convergence in measure)是實變函式論中重要的收斂概念之一。...
依機率收斂,convergence in probability,別稱隨機收斂,套用於機率論與數理統計。...... 依機率收斂是測度論中的依測度收斂概念在機率論中的特例。[1] 依...
設μ是X上的正測度,X上的復可測函式序列{fn}稱為依測度收斂於可測函式f,如果對每一個ε〉0,存在一個對應的N,使得μ({x:|fn(x)-f(x)|〉ε})〈ε...
機率論中的伯努利大數律就是最早闡明隨機試驗中某事件發生的頻率依機率收斂於其機率()的。依機率收斂相當於測度論中的依測度收斂。 對≥1,若-的階絕對矩(見矩...
若m(E)<+∞,{fn(x))是E上可積函式列,且依測度收斂於f(x),又{fn(x)}的積分具有等度絕對連續性,則f(x)是可積函式,且...
1 定理定義 2 驗證推導 3 反向法圖引理 4 定理推廣 ▪ 任意實值函式 ▪ 逐點收斂 ▪ 依測度收斂 法圖引理定理定義 編輯 設 為一個測度空間, ...
§3.2可測函式列的收斂性與Lebesgue可測函式的結構1.測度空間和“幾乎處處”(128)2.依測度收斂(130)3.完全測度空間上的可測函式列的收斂(139)4.L,ebesgue...
則S(E)是以日·}}為準範數的弗雷歇空間,且在其中依準範數的收斂等價於依測度收斂.可以在測度空間上,類似地建立S空間.詞條標籤: 科學 ...
也可以引進平均收斂等概念,並且與幾乎處處收斂、依測度收斂、近於一致收斂的關係也一樣,僅需做明顯的文字和記號修改。中文名 抽象積分 外文名 abstract integral ...
,則S(E)是以||・||為準範數的弗雷歇空間,且在其中依準範數的收斂等價於依測度收斂。可以在測度空間上,類似的建立S空間。 [1] 函式...
4.1測度論的起源 4.1.1為什麼要了解測度 4.1.2勒貝格測度簡介 4.2可測函式 4.2.1可測函式的定義 4.2.2可測函式的性質 4.2.3依測度收斂 4.3勒貝格積分簡介 4.3...
依機率收斂是測度論中的依測度收斂概念在機率論中的特例。[3] 依機率收斂是一種常見的收斂性質。依機率收斂比依分布收斂更強,比平均收斂則要弱。...
測度基礎上的積分,導致了與微積分中函式序列的點點收斂和一致收斂不同的一些新的重要收斂概念的產生,它們是幾乎處處收斂、度量收斂(亦稱依測度收斂)、積分平均收斂等...
3 依測度收斂、L空間 1.基本概念 2.凸函式·幾個重要的積分不等式 3.Lp空問的定義 4.復可測函式空間 5.依測度收斂與依距離收斂的等價性 6.空間...
§4.3依測度收斂§4.4盧津定理§4.5單調函式與有界變差函式§4.6絕對連續函式習題4附錄4.1葉戈羅夫生平附錄4.2盧津生平第5章積分§5.1非負簡單函式的積分§5.2非...
2.4.2 依測度收斂2.4.3 依分布律收斂2.5 補充與習題第三章 數學期望與積分3.1 積分的定義和性質3.1.1 積分的定義3.1.2 積分的性質3.2 收斂定理...
使讀者能夠了解實變函式論中結果成立的拓撲背景,也便於讀者繼續深入一般測度論的...4.3.2依測度收斂和幾乎處處收斂...864.3.3可測函式的構造...89 習題4......
4.3 依測度收斂性4.4 Lusin(魯津)定理4.5 例題選講習題四5 Lebesgue積分5.1 非負可測簡單函式的積分5.2 非負可測函式的積分5.3 一般可測函式的積分...
3.5 廣義測度習題34 可測函式4.1 可測函式的定義及簡單性質4.2 葉果洛夫(Egoroff)定理4.3 可測函式與連續函式之間的關係4.4 依測度收斂...
4 3依測度收斂性694 4Lusin(魯津)定理724 5例題選講74習題四795Lebesgue積分815 1非負可測簡單函式的積分815 2非負可測函式的積分82...
