基本介紹
- 中文名:么正變換
- 外文名:Unitary transformation
- 學科:數學
- 方法:是使用么正算符所做的變換
- 本質:是兩個希爾伯特空間之間的同構
- 相關名詞:么正算符
簡介
屬性
算符么正變換


基矢么正變換






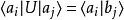



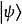


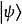


反么正變換
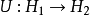









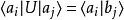



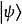


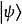


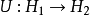

在數學中,么正變換是保留內積的變換:變換之前的兩個向量的內積等於其轉換後的內積。么正變換是使用么正算符所做的變換,有對基矢的變換,有對算符的變換。更...
在泛函分析中,么正規範是定義在希爾伯特空間上的有界線性算符U : H → H,滿足如下規律U∗U=UU∗=I,其中 U∗ 是 U的厄米轉置, 而 I : H → H...
10.8從獨立粒子坐標到雅可比坐標的變換的么正算符 習題(第9,10章) 第11章費米系統的IWOP技術與套用 11.1 費米相干態與費米體系的IWOP技術 11.2 Gr...
根據這個定理,任何對稱性操作都是希爾伯特空間上的一個么正變換或者反么正變換。更準確的說,這個定理描述的是在一個復的希爾伯特空間H上,如果對任意的 都有滿射 ...
3.2 內積空間、正交變換、么正變換 3.3 角動量算符與空間轉動群的表示 3.4 時間平移群與波函式的演化 3.5 內積空間 3.6 轉動群的SU(2)表示旋量波函...
既然計算機中的每一步操作都可以改造為可逆操作,那么在量子力學中,它就可以用一個么正變換來表示。早期量子計算機,實際上是用量子力學語言描述的經典計算機,並沒有...
由定域規範變換下不變性所要求存在的場,稱為規範場。變換 ⑵在數學上構成單參數的么正變換群U⑴,這種變換往往被稱為U⑴定域規範變換。電磁場就是U⑴定域規範...
四維動量的時間分量是能量,如果時間反演操作是么正變換的話則能量將在時間反演下變號,而這是不可能的,因為能量恆正。 在量子力學中能量出現在相位因子exp(-iEt)...
“轉移”到EPR對的第二個粒子上,只要根據經典通道傳送的Bell基測量結果,對EPR的第二個粒子的量子態施行適當的么正變換,就可使這個粒子處於與待傳送的未知態完全...
與經典計算機不同,量子計算機可以做任意的么正變換,在得到輸出態後,進行測量得出計算結果。因此,量子計算對經典計算作了極大的擴充,在數學形式上,經典計算可看作是...
§2.10么正變換,厄米變換§2.11子空間§2.12本徵矢量和本徵值§2.13主軸變換§2.14矩陣的外積及其它第三章抽象群理論§3.1群的定義...
5.8 四波混頻的么正變換算符 5.9 用壓縮的觀點看轉動——角動量算符的新玻色實現 5.10 角動量算符的新玻色實現的套用 5.11 用糾纏態表象求解含時參量放...
代表不同的味,則理論在么正變換下保持形式不變,這裡U=(Uij)構成三行三列的么正矩陣。 [2] 量子色動力學色規範場 編輯 假設上述強作用的 SU(3)對稱性是定...
15 可見這個變換矩陣是一種么正矩陣,式⑻中兩種表象之間基矢的變換是一個么正變換。態態的表象表示⑴ 坐標表象以坐標算符的本徵態為基底構成的表象稱為坐標表象...
為希耳伯空間的基矢所構成的表象稱為耦合表象。因此,矢量耦合係數也就是無耦合表象與耦合表象的基矢之間的么正變換矩陣的矩陣元。角...
4.5 么正變換 第5章 近似方法 5.1 非簡併定態微擾理論線性諧振子和基態氫原子的極化, 5.2 簡併定態微擾理論Stark效應 5.3 變分法氦原子基態 5.4...
(IWOP技術)以嶄新的視角和方法研究量子態在相空間中的準幾率分布函式表示、演化、重構,以及經典函式量子化、經典變換與量子么正變換的關係,以促進和深化量子統計的...
第7章 量子力學的矩陣形式與表象變換 *7.1 量子態的不同表象,么正變換 *7.2 力學量(算符)的矩陣表示 *7.3 量子力學的矩陣形式 7.3.1 Schrodinger方程 ...
(變化)後的狀態是對稱的,然後將聯合測量的信息通過經典信道傳送給接收方,接收方根據接收到的信息對坍塌的粒子進行么正變換(相當於逆轉變換),即可得到與傳送方完全...
[等人提出了一種3個輸入變數的綜合方法.Iwama等人給出了CNOT電路的綜合規則,提出CNOT門序列順序變化的規則,通過將實現麼變換的相鄰且相同的門消除,最終實現可逆...
20.1.2么正變換 20.2電流公式 20.3隧穿電導 20.4鐵磁隧道結的磁阻效應 習題 參考文獻 附錄A巨觀極限的威克定理 附錄B電子氣凝膠模型的哈密頓量 附錄C約束條...
14.5反么正變換與Dirac符號的局限性第15講可觀測性、完備性與中心場塌縮——三者的含義與關聯15.1力學量的可觀測性與其算符本徵函式族的完備性...
