矢量耦合係數是兩個角動量耦合時,它們的本徵函式的組合係數。從數學的角度,克萊布希-戈登係數出現在緊李群的表示論中,它研究的是兩個不可約表示的張量積如何分解成不可約表示的直和。
基本介紹
- 中文名:矢量耦合係數
- 外文名:vector coupling coefficient
- 定義:角動量耦合的本徵函式的組合係數
- 套用學科:量子力學術語
- 範疇:數理科學
- 涉及:本徵函式
概念,基本原理,
概念
矢量耦合係數是兩個角動量耦合時,它們的本徵函式的組合係數。從數學的角度,克萊布希-戈登係數出現在緊李群的表示論中,它研究的是兩個不可約表示的張量積如何分解成不可約表示的直和。克萊布希-戈登係數因阿爾弗雷德·克萊布希和保羅·哥爾丹而得名。
基本原理
對於由兩個粒子組成的體系,用 、
、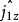 和
和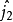 、
、 分別表示兩個粒子的角動量算符和角動量的
分別表示兩個粒子的角動量算符和角動量的 分量算符,
分量算符,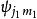 和
和 分別表示算符
分別表示算符 、
、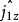 和
和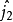 、
、 的共同本徵函式。若以乘積
的共同本徵函式。若以乘積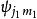
 作為希耳伯空間的基矢,則這兩個粒子相耦合的體系的波函式
作為希耳伯空間的基矢,則這兩個粒子相耦合的體系的波函式 (它是算符
(它是算符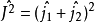 和
和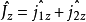 的共同本徵函式)可以表達成:
的共同本徵函式)可以表達成:

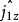
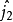


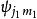


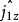
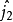

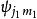


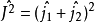
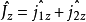
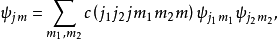
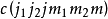
以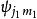
 為希耳伯空間的基矢所構成的表象稱為無耦合表象。以
為希耳伯空間的基矢所構成的表象稱為無耦合表象。以 為希耳伯空間的基矢所構成的表象稱為耦合表象。因此,矢量耦合係數也就是無耦合表象與耦合表象的基矢之間的么正變換矩陣的矩陣元。
為希耳伯空間的基矢所構成的表象稱為耦合表象。因此,矢量耦合係數也就是無耦合表象與耦合表象的基矢之間的么正變換矩陣的矩陣元。
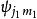


角動量 = 轉動慣量 * 角速度其中,角動量和角速度是矢量,其方向按一般的約定是,與旋轉軸相同,指向右手螺旋方向(右手握旋轉軸,四指指向旋轉方向,拇指向上方向為角動量和角速度矢量的方向)。

