量子色動力學

量子色動力學（Quantum Chromodynamics，簡稱QCD）是在阿德勒、伯約肯以及其他人工作的基礎上，在1972年由蓋爾曼和弗里奇所創立。它是一種強相互作用的規範理論，它描述組成強作用粒子（強子）的夸克和與色量子數相聯繫的規範場的相互作用，可以統一地描述強子的結構和它們之間的強相互作用，被認為是有希望的強作用基本理論。

基本介紹

• 中文名：量子色動力學
• 外文名：Quantum Chromodynamics
• 作用：描述夸克之間強相互作用
• 套用領域：量子力學
• 創立時間：1972年
• 創立者：蓋爾曼和弗里奇

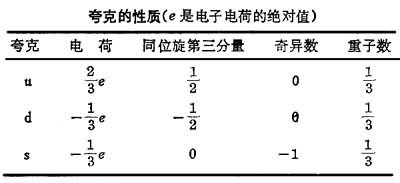
強子結構

按照夸克模型，所有重子都由三個夸克組成，所有介子都由一對正反夸克組成。夸克的自旋為1/2。為組成實驗觀察到的重子和介子，須認為夸克有許多種，在文獻上稱為夸克的味。為使重子內部波函式有費密統計所要求的全反對稱性，並說明重子由三個夸克組成，人們提出夸克還具有另一種內部自由度，它可以取三種不同的狀態，人們借用光學中的辭彙稱它們有三種不同的色。

重子中的三個夸克各帶不同的色。介子中的正反夸克對帶相反的色量子數。重子和介子都不帶色量子數，它們是“白色”的。三種色夸克在強作用中的性質完全相似，因此強作用有與此相應的對稱性。以ψia代表夸克場，其中i=1，2，3代表三種色，a=1，2，3……代表不同的味，則理論在么正變換下保持形式不變，這裡U=(Uij)構成三行三列的么正矩陣。

色規範場

假設上述強作用的 SU(3)對稱性是定域的對稱性，即當群參量Θα是時空坐標t和x的函式時，理論仍保持不變，就引導到色規範場的概念。在這個規範理論中，除夸克場ψia外還有八個規範場Aα(α=1，2，...…，8)，分別與八個守恆流耦合。

如果假設上述強作用的 SU(3)對稱性是定域的對稱性，即當群參量Θ_α是時空坐標t和x的函式時，理論仍保持不變，就引導到色規範場的概念。在這個規範理論中，除夸克場ψ_ia外還有八個規範場A_α(α=1，2，...…，8)，分別與八個守恆流耦合。SU(3)定域規範不變的要求唯一地確定拉氏函式密度的形式

式中

是SU(3)群的結構常數，它們由下式定義：

g是規範作用的耦合常數,m_α是味a的夸克的質量,它與夸克的色無關。由以上拉氏函式出發的量子場論就是量子色動力學。由於都是規範理論，它與電磁作用的基本理論量子電動力學有不少共同之處，但是也有重要的差別。與量子電動力學中傳遞電磁作用的光子相對應，這裡有八個零質量的自旋為1的規範粒子。它們可以被誇克所吸收或發射，並傳遞夸克之間的色作用力。這種力把夸克束縛在強子中，所以這些規範粒子也稱為膠子。這種作用力也是兩個強子之間的通常的強作用力的來源，後者是不帶色量子數的強子之間的剩餘色作用。在上面寫出的拉氏函式密度中描述規範場 與夸克的相互作用的項是 ，這裡

相當於量子電動力學中電子所帶的電流 ，因此可認為是夸克所帶的一部分色流。在量子電動力學中電流J_μ守恆；光子本身不帶電荷，兩個光子之間不能通過光子的傳遞而相互作用。與量子電動力學的情況不同，在量子色動力學中膠子本身也帶色量子數。夸克所帶的一部分色流單獨 並不守恆，只有它與膠子場所帶色流之和才是守恆的。因此膠子場與色流的相互作用也包含膠子場的自作用。這表現在拉氏函式中有三個和四個A_μ場相乘的項。由於有膠子場的自作用，兩個膠子之間也存在由膠子傳遞的強作用力。這種差別的根源在於量子電動力學的規範群U(1)的元素是可以交換的，而量子色動力學的規範群 SU(3)的元素是不可交換的，因而

規範理論

微擾量子色動力學與漸近自由。量子色動力學屬於規範理論，因而是可重正化的。它的微擾論展開式可以計算到高階。在其他的強作用量子場論中，由於耦合常數大，微擾論展開式不能用來作可靠的計算。在這方面量子色動力學有它獨特之處。在量子電動力學中，由於真空極化的禁止作用，使電子的有效電荷隨著對電子距離減小而變大。

重正化

性質

非交換群規範場理論以外的其他可重正化場論幾乎都有類似的性質，它們的有效耦合常數隨距離減小而增加，即在小距離內作用變強。非交換群規範理論則不同。研究表明，規範場的自作用能夠產生相反的效果，使得放在真空中的色荷吸引真空中產生的規範粒子，在它的周圍聚集相同的色荷，造成反禁止的效應。

種類

在夸克的味不超過16種時，真空中膠子分布所產生的反禁止效應超過夸克對產生的禁止效應。在這種情況下量子色動力學有所謂漸近自由的性質，即隨著時空距離的變小相互作用變弱，有效耦合常數隨距離趨於零。按照測不準關係，小的時空距離相應於大的能量動量。某些高能過程的物理量主要與小的時空距離有關。對於這些物理量，量子色動力學中按有效耦合常數的冪次的微擾論展開式，在高能下很快地收斂，因此可以作可靠的計算。迄今為止，別的強作用理論都由於沒有小參量而無法作可靠的近似，量子色動力學在這方面是唯一的例外。

無關性

強作用的近似標度無關性 70年代中, 在輕子的深度非彈性散射的單舉截面、正負電子對撞產生強子的總截面及這些過程中產生的強子噴注等一系列高能實驗中，發現強作用有一些未曾預料到的性質。所謂輕子的非彈性散射是指電子e與核子N碰撞而產生一些強子，e+N→e+N+強子，或中微子v與核子N碰撞轉化成μ子和一些強子，v+N→μ+強子。這兩個過程分別是電磁作用和弱作用過程，同時也有強作用參加。如果在碰撞中輕子動量傳遞的二次方q2和能量損失(mN 是核子的質量)都很大，則這個過程稱為深度非彈性散射。在單舉截面中，只測量輕子。

質心繫總能量W

動量

因此這個截面只是 q2和 v 的函式。單舉截面決定於幾個稱為結構函式的無量綱的量。這些結構函式只與強作用有關。實驗發現在 q2和v都很大時它們近似地只依賴於比值x=q2/2v,對固定的x,它們隨q2的變化很緩慢。正負電子對撞產生強子和產生 μ子對的總截面的比 r是正負電子對的質心系總能量W 的函式。實驗發現，在W大時R近似地是常數（除在某些產生新粒子的閾能附近以外）。這些及其他一些實驗結果可以解釋為強作用中沒有一個在高能下起作用的固有的能量標度，在有關的能量、動量都很高時，粒子的質量及其他有質量或能量量綱的常數都可以忽略，因此只依賴於強作用的無量綱的量都只是有關的能量、動量的比的函式，而不是某個能量、動量與某個有量綱常數的比的函式。這就是實驗所揭示的強作用在高能下的近似。

標度無關性

然而在可重正化場論微擾展開式的高階中總是要出現形式的因子，這裡g是耦合常數，E是某個能量,μ是粒子質量或由重正化引進的參量。這樣的項在E2很大時並不能忽略。因此至少在微擾論範圍內一般的可重正場論沒有無標度性。但是對量子色動力學這樣的漸近自由的理論,有效耦合常數在有關的能量、動量趨於無窮大時趨於零。因此，在上述高能過程中標度無關性在極限下可以保持或只有輕微的破壞。這種定性的成功使得量子色動力學受到人們的重視。量子色動力學的微擾論計算結果與輕子深度非彈性散射、電子正電子碰撞產生強子、噴注現象等高能過程的實驗數據是一致的。理論與實驗在各種過程中的定量比較還需要繼續進行。

強子結構

在量子色動力學中夸克的質量不大，膠子的質量為零，它們應當很容易產生。因此必須解釋為什麼沒有在實驗中觀察到這些粒子。作為強作用的基本理論，人們還需要量子色動力學來得到強子譜和強子的結構，這些問題不能在微擾論的範圍內得到解答。人們構想夸克和膠子這樣的帶色量子數的粒子是由於規範場相互作用的動力學的原因而被禁閉在強子半徑10-13cm的範圍內。只有強子這樣的白色的複合粒子才能作為自由粒子而出現。這種色量子數的禁閉或者是絕對的或則是近似的。人們從不同的角度給出論據，企圖說明色的禁閉在量子色動力學中是成立的。

強子結構

論據

一些論據給出如下的圖像。與電磁場的電力線相似，色規範場也可以用力線描述。兩個相反的色荷之間有力線相連線。在量子色動力學中的力線不像兩個相反電荷之間的電力線那樣分散在空間而是集中在兩個色荷的連線上形成一根弦。人們把這種情況與穿入第二類超導體中的磁力線相比，這時磁力線受超導體的排斥而形成細管。規範場力線的弦中帶有正比於弦的長度的能量，當兩個色荷之間的距離增加趨於無窮時，弦所帶的能量也將趨於無窮。在此以前弦可以斷裂而產生一對新的相反的電荷。每段弦的兩端都有一對相反的色荷。無論是哪種情況，都不能把兩個色荷分開到大的距離。因此這個圖像給出色禁閉。對這個圖像的一個支持來自格點規範理論。在格點規範理論中連續的時空被離散的格點所代替。規範場和與它作用的費密場分別定義在聯接相鄰格點的線和格點本身所組成的點陣上。拉氏函式滿足離散格點上的規範不變性。當兩個格點間的距離a趨於零時，格點規範理論趨於連續時空的規範理論。與連續時空規範理論的漸近自由相對應，在格點規範理論中，如果固定某個物理量的數值則耦合常數g隨格點間的距離 a減小而減小。在a趨於零時格點規範理論可以用弱耦合展開，它趨於連續理論的微擾論。

微擾論

在a大時g的值大，應當用強耦合展開，即展開成的冪級數。在強耦合極限下證明了非交換群格點規範理論中兩個色荷之間的力線聚集成弦，因而有色禁閉。為證明連續理論有色禁閉還需要證明在耦合由強變弱時色禁閉的性質不消失。在電子計算機上用蒙特－卡羅法。對格點數不多的點陣進行研究的結果表明，對於一段中間的g值計算結果可以同時與色禁閉的弦和連續理論的漸近自由微擾展開式一致。這個結果支持連續時空的規範理論有色禁閉的性質。格點規範理論的研究沒有發現在 g變小的過程中存在解除色禁閉的“相變”。雖然如此，連續時空規範理論的色禁閉還只是一種有某些根據的猜測，這是量子色動力學中還存在的一個基本問題。至於強子譜的研究更是處於開始的階段。