研究物理或數學過程的一種隨機模型的計算方法。蒙特－卡羅法可以用來求解兩類問題。第一類問題稱之為機率問題，用直接模擬某種物理過程的方法解決。第二類問題，是所謂定數問題。在解定數問題時，必須把問題化為相適應的能作模擬的機率問題。
基本介紹
- 中文名：蒙特·卡羅方法
- 外文名：Monte Carlo method
- 別稱：統計模擬方法
正文,發展,
正文
研究物理或數學過程的一種隨機模型的計算方法。蒙特－卡羅法是以隨機抽樣技巧作為工具的一門近代數值分析的學科。
蒙特－卡羅法的思想提出雖然較早，但系統性的研究實開始於1944年前後。當時由於研製核子彈，需要研究中子在裂變物質中的輸運，提出了一些不易用一般數學方法求解的問題。J.馮·諾埃曼、S.烏拉姆和E.費密等發展了這個用直接模擬物理過程的方法，解決了這些當時不易解決的難題。在研究宇宙線簇射中的問題時，也使用了這個方法。
蒙特－卡羅法可以用來求解兩類問題。第一類問題稱之為機率問題，用直接模擬某種物理過程的方法解決。為了說明求解機率問題的方法，現舉一個γ射線對有限厚度的平板媒質的穿透問題(圖1)作為例子。
蒙特－卡羅法為了簡單起見，只限於在垂直於平板媒質的平面內討論。假定γ射線是單能的，發出光子的波長為λ。單向發射與平板媒質面的法線所成的角度為Θ。則光子從進入媒質的點出發，在有限平板媒質中第一次發生碰撞的位置，可由機率密度
決定, 其中(λ)是波長為λ的光子的總截面。具體地說，是這樣決定的，在電子計算機上產生一隨機數ξ，由下列公式可以決定，
其次，根據媒質對光子的吸收截面，決定它是否被吸收。如α(λ)是吸收截面，(λ)是散射截面, 當γ射線能量不高時，可以簡單地認為
再由電子計算機產生一隨機數ξ，如，則光子被吸收，不然則未被吸收。如被吸收，則須重取一光子，從頭開始這個過程；如未吸收，則從克萊因－仁科公式和康普頓公式（見光的量子理論）決定光子經過一次散射後的波長λ，和光子散射前與散射後的方向之間的夾角，由此可定出光子散射後的方向。決定λ與的隨機抽樣技巧，不擬在此多述。連續使用這樣的過程，就可研究光子在媒質中的行為。所以追蹤一個光子行為的過程是這樣的：先定光子的碰撞位置，然後再定光子的波長改變和方向改變，對一個光子一直追蹤下去，直到它被吸收，或被反射出這個平板媒質，或穿透過這個平板媒質。
以後再取一個光子，用上面所述的辦法進行追蹤。如果所取的總的光子樣品數目為，其中個光子通過平板媒質，則穿透幾率便為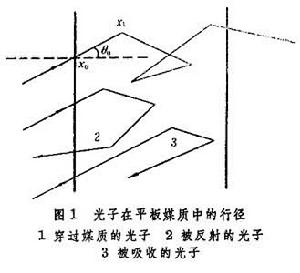
蒙特－卡羅法
蒙特－卡羅法
蒙特－卡羅法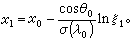
蒙特－卡羅法
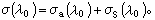蒙特－卡羅法
蒙特－卡羅法的思想提出雖然較早，但系統性的研究實開始於1944年前後。當時由於研製核子彈，需要研究中子在裂變物質中的輸運，提出了一些不易用一般數學方法求解的問題。J.馮·諾埃曼、S.烏拉姆和E.費密等發展了這個用直接模擬物理過程的方法，解決了這些當時不易解決的難題。在研究宇宙線簇射中的問題時，也使用了這個方法。
蒙特－卡羅法可以用來求解兩類問題。第一類問題稱之為機率問題，用直接模擬某種物理過程的方法解決。為了說明求解機率問題的方法，現舉一個γ射線對有限厚度的平板媒質的穿透問題(圖1)作為例子。
蒙特－卡羅法為了簡單起見，只限於在垂直於平板媒質的平面內討論。假定γ射線是單能的，發出光子的波長為λ。單向發射與平板媒質面的法線所成的角度為Θ。則光子從進入媒質的點出發，在有限平板媒質中第一次發生碰撞的位置，可由機率密度
決定, 其中(λ)是波長為λ的光子的總截面。具體地說，是這樣決定的，在電子計算機上產生一隨機數ξ，由下列公式可以決定，
其次，根據媒質對光子的吸收截面，決定它是否被吸收。如α(λ)是吸收截面，(λ)是散射截面, 當γ射線能量不高時，可以簡單地認為
再由電子計算機產生一隨機數ξ，如，則光子被吸收，不然則未被吸收。如被吸收，則須重取一光子，從頭開始這個過程；如未吸收，則從克萊因－仁科公式和康普頓公式（見光的量子理論）決定光子經過一次散射後的波長λ，和光子散射前與散射後的方向之間的夾角，由此可定出光子散射後的方向。決定λ與的隨機抽樣技巧，不擬在此多述。連續使用這樣的過程，就可研究光子在媒質中的行為。所以追蹤一個光子行為的過程是這樣的：先定光子的碰撞位置，然後再定光子的波長改變和方向改變，對一個光子一直追蹤下去，直到它被吸收，或被反射出這個平板媒質，或穿透過這個平板媒質。
以後再取一個光子，用上面所述的辦法進行追蹤。如果所取的總的光子樣品數目為，其中個光子通過平板媒質，則穿透幾率便為
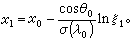蒙特－卡羅法蒙特－卡羅法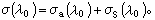蒙特－卡羅法蒙特－卡羅法蒙特－卡羅法ρ=m/N。
蒙特－卡羅法解決的第二類問題，是所謂定數問題。在解定數問題時，必須把問題化為相適應的能作模擬的機率問題。
這裡舉求定積分的問題作為例子。求定積分是一個定數問題，它可以化為打靶問題，而打靶問題是機率問題。例如計算定積分
假定()在0≤≤1之間是處於0與1之間,即0<()<1。積分為曲線=(),=0,=1,=0所包的面積之值。
要求積分，可以先設制一個正方靶(0≤≤1；0≤≤1)在這正方靶內,作曲線=()(圖2)，並對這靶投射黑點。假定投射在單位正方形靶內任意點(,)的機率相等，如果點落在曲線=()的下面或剛落在這曲線上【即當≤()】，則認為事件A實現；如果點落在曲線=()的上方【即≤()】，則認為事件A不實現。可以證明，事件A實現的機率即是這積分之值。
蒙特－卡羅法根據上面的思想，可以在電子計算機上具體模擬射靶過程。在電子計算機上產生均勻分布於 (0,1)區域內的兩個獨立隨機變數ξ和η，用來表示射靶試驗所射到的點的坐標。因為隨機變數在區域 (0,1)內出現的機會均等，而且它們之間是彼此獨立的,因此所產生的點(ξ,η)顯然均勻地落在正方形內。
從上述產生的隨機數ξ與η，定義
假定試驗進行了次，則求得事件A實現的機率近似地為積分的值
蒙特－卡羅法
蒙特－卡羅法
蒙特－卡羅法
這裡舉求定積分的問題作為例子。求定積分是一個定數問題，它可以化為打靶問題，而打靶問題是機率問題。例如計算定積分
假定()在0≤≤1之間是處於0與1之間,即0<()<1。積分為曲線=(),=0,=1,=0所包的面積之值。
要求積分，可以先設制一個正方靶(0≤≤1；0≤≤1)在這正方靶內,作曲線=()(圖2)，並對這靶投射黑點。假定投射在單位正方形靶內任意點(,)的機率相等，如果點落在曲線=()的下面或剛落在這曲線上【即當≤()】，則認為事件A實現；如果點落在曲線=()的上方【即≤()】，則認為事件A不實現。可以證明，事件A實現的機率即是這積分之值。
蒙特－卡羅法根據上面的思想，可以在電子計算機上具體模擬射靶過程。在電子計算機上產生均勻分布於 (0,1)區域內的兩個獨立隨機變數ξ和η，用來表示射靶試驗所射到的點的坐標。因為隨機變數在區域 (0,1)內出現的機會均等，而且它們之間是彼此獨立的,因此所產生的點(ξ,η)顯然均勻地落在正方形內。
從上述產生的隨機數ξ與η，定義
假定試驗進行了次，則求得事件A實現的機率近似地為積分的值
蒙特－卡羅法蒙特－卡羅法蒙特－卡羅法。
其他如線性代數方程組、微分方程、積分方程均可用蒙特－卡羅法求解。此外，它還可以很方便地用於多維、多因素問題的計算。
這方法不僅在原子能套用中大量使用，在粒子物理、原子核物理、固體物理、統計物理、高分子化學、軍事科學、氣象科學、醫學、地質學、線性規劃等領域均已廣泛套用。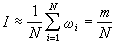
蒙特－卡羅法
這方法不僅在原子能套用中大量使用，在粒子物理、原子核物理、固體物理、統計物理、高分子化學、軍事科學、氣象科學、醫學、地質學、線性規劃等領域均已廣泛套用。
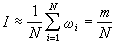蒙特－卡羅法發展
蒙特－卡羅法在近30年來所以能有這樣大的發展，與快速電子計算機的廣泛使用分不開。凡用蒙特－卡羅法模擬一個問題時，往往需要進行大量的抽樣，而抽樣過程靠電子計算機進行。如果要求計算結果的機率誤差愈小，所抽的樣品應愈多，因此計算量相當大，沒有現代計算技術，很難構想蒙特－卡羅法會有這樣的發展。可以預料，隨著計算技術的進一步發展，蒙特－卡羅法將會有更大的發展。
