基本介紹
- 中文名:孫子定理
- 外文名:Chinese remainder theorem(CRT)
- 分類:數學
- 提出:孫子
- 問題:一元線性同餘方程組
- 又名:餘數定理
公式
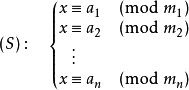
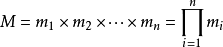
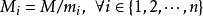

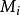
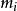
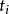
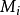


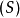
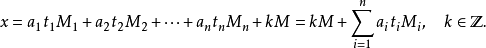

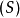



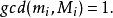
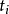
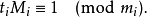
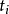
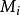
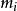

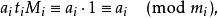
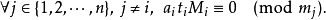



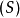

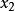
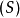




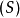
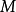
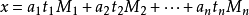

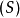
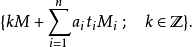
文獻
交換環上推廣
主理想整環

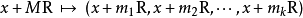



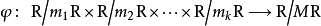
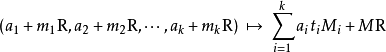

一般的交換環
中國餘數定理一般指本詞條
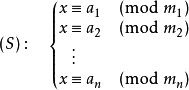
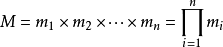
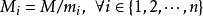

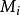
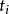
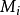


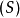
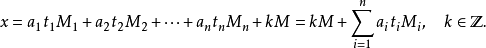

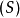



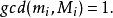
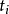
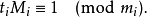
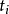
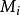
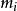

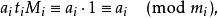
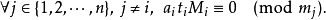



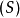

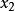
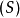




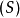
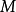
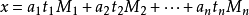

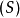
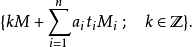

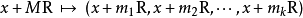



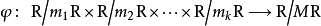
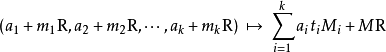

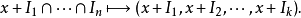
孫子定理是中國古代求解一次同餘式組(見同餘)的方法。是數論中一個重要定理。又稱中國餘數定理。一元線性同餘方程組問題最早可見於中國南北朝時期(公元5世紀)的數學...
《數書九章》系統地論述了一次同餘式組解法的基本原理和一般程式,於12世紀末流傳到歐洲,被稱為“中國剩餘定理”(CRTChineseRemainder Theorem),這是最早的餘數系統(...
下卷第28題“物不知數”為後來的“大衍求一術”的起源,被看作是中國數學史上最有創造性地成就之一,稱為中國餘數定理:今有物,不知其數。三三數之,剩二;...
中國餘數定理,也稱中國剩餘定理,孫子剩餘定理。 從《孫子算經》到秦九韶《數書九章》對一次同餘式問題的研究成果,在19世紀中期開始受到西方數學界的重視。1852年,...
31.5 中國餘數定理31.6 元素的冪31.7 rsa公鑰加密系統*31.8 素數的測試*31.9 整數的因子分解第32章 字元串匹配32.1 樸素的字元串匹配算法...
例26 中國餘數定理3907.4.2 調頻法測距[8,38]3927.5 主瓣雜波398例27 高度線回波398例28 採用脈衝都卜勒雷達進行飛彈逼近告警...
近10年內撰寫數學論文多篇,其中,在省級刊物上發表的有《從中國餘數定理說起》(《國中生數學輔導》1990年第9期)、《穿洞過橋,行程知多少》(《國中生數學學習》...
3.5 中國餘數定理3.6 單向函式與單向暗門函式3.7 習題第4章 分組加密體制4.1 分組密碼4.1.1 分組密碼概述4.1.2 分組密碼設計思想...
9.1.1差分濾波多基線InSAR處理185 9.1.2中國餘數定理多基線InSAR處理192 9.1.3套用貝葉斯估計方法的多基線InSAR處理199 9.2多頻率InSAR202 [1] 參考...
用歐幾里得算法求兩整數的GCD、LCM;求解模線性方程;中國餘數定理;質因數分解等。 參考書目:《實用算法的分析與程式設計》,吳文虎,清華大學出版社 典型例題:1019 ...
中國餘數定理 貝爾方程 阿基米德分牛問題 五家共井 百雞問題 費爾馬大定理被證明了! 有趣的“翹翹板”法 計算機怎么解方程? 病態方程 函式 從費爾...
6.3.4費馬小定理與歐拉定理···1576.4討論及擴展閱讀···1596.5要點回顧·...7.5.2使用中國餘數定理的快速加密···1747.6尋找大素數···...
5.7 韓信點兵——中國餘數定理5.8 魔盤第六章 通用方法性知識套用例子(2)6.1 13球問題6.2 奇數幻方6.3 華容道第七章 權威論文、著名博士論文淺說列舉7.1 ...
在保持第1版結構的指導思想下,增加了若干新內容,包括彩虹表及其在字典攻擊中的套用、rc4序列密碼安全性討論、中國餘數定理及其在證明rsa算法正確性的套用、漩渦散列...
10.6 中國餘數定理10.7 PRF選擇技術參考文獻習題第11章 機載雷達對運動目標的觀測11.1 低、中、高PRF11.2 高PRF雜波模型11.3 空-空雷達...
3.4.1費馬定理3.4.2歐拉定理3.4.3本原元3.5中國餘數定理3.6單向函式與單向暗門函式習題第4章分組加密體制4.1分組密碼4.1.1分組密碼概述...
3.4.1費馬定理3.4.2歐拉定理3.4.3本原元3.5中國餘數定理3.6單向函式與單向暗門函式習題第4章分組加密技術4.1分組密碼4.1.1分組密碼概述...
一般的乘積碼輸出碼字時都是按行順序或列順序輸出,對於循環乘積碼用m(i,j)表示矩形陣列元素的輸出順序,則根據中國餘數定理對矩形陣列的傳送碼字排序即可得到循環...
