簡介
概念定義
用符號“<”(或“≤”),“>”(或“≥”),“≠”連線的式子叫做不等式。(不等式中可以含有未知數,也可以不含。)
用不等號連線的,含有一個未知數,並且未知數的次數都是1,未知數的係數不為0,左右兩邊為整式的式子叫做一元一次不等式(linear ineqality with one unknown)。
一元一次不等式滿足的條件:不等號的兩邊都是整式;不等式中只含有一個未知數;未知數的次數是1。
一元一次不等式是最簡單的代數不等式,它是整式形式的不等式,比如
不是一元一次不等式。因為未知數x在分母中,使得該不等式的左邊不是整式形式。
不等式性質:
(1)不等式的兩邊都加上(或減去)同一個數(或式子),不等號的方向不變。
(2)不等式的兩邊都乘以(或除以)同一個正數,不等號的方向不變。
(3)不等式的兩邊都乘以(或除以)同一個負數,不等號的方向改變。
數字語言簡潔表達不等式的性質:
【1.性質1:如果a>b,那么a±c>b±c)】
【2.性質2:如果a>b,c>0,那么ac>bc(或a/c>b/c)】
【3.性質3:如果a>b,c<0,那么ac<bc(或a/c<b/c)】
一般步驟:
(1)去分母:根據不等式的性質2和3,把不等式的兩邊同時乘以各分母的最低公倍數,得到整數係數的小等式。
(2)去括弧:根據上括弧的法則,特別要注意括弧外面是負號時,去掉括弧和負號,括弧裡面的各項要改變符號。
(3)移項 :根據不等式基本性質1,一般把含有未知數的項移到不等式的左邊,常數項移到不等式的右邊。
(4)合併同類項。
(5)將未知數的係數化為1 :根據不等式基本性質2或3,特別要注意係數化為1時,係數是負數,不等號要改變方向。
(6)有些時候需要在數軸上表示不等式的解集
不等式解集
一個有未知數的不等式的所有解,組成這個不等式的解集。例如﹕不等式x-5≤-1的解集為x≤4;不等式x﹥0的解集是所有正實數。求不等式解集的過程叫做解
不等式。
一元一次不等式的解集是一個符合某一個特定條件的一元一次不等式的解的集合,一元一次不等式的解和一元一次不等式的解集是兩個不同的概念。它們是從屬關係。
將一元一次不等式化為ax>b的形式
(1)若a>0,則解集為x>b/a。
(2)若a<0,則解集為x<b/a。
表示:
(1) 用不等式表示:一般地,一個含未知數的不等式有無數個解,其解集是一個範圍,這個範圍可用最簡單的不等式表達出來,例如:x-1≤2的解集是x≤3。
(2) 用數軸表示:不等式的解集可以在數軸上直觀地表示出來,形象地說明不等式有無限多個解,用數軸表示不等式的解集要注意兩點:一是
定邊界線;二是定方向。
(3)能使不等式成立的未知數的值,叫做不等式的解。
不等式組
(1) 一般地,關於同一個未知數的幾個一元一次不等式合在一起,就組成一個一元一次不等式組。
(2)一元一次不等式組中各個不等式的解集的公共部分,叫做這個一元一次不等式組的解集。求
不等式組解集的過程,叫做解不等式組。
1. 代數式大小的比較:
(1) 利用數軸法;
(2) 直接比較法;
(3) 差值比較法;
(4) 商值比較法;
(5) 利用特殊比較法。(在涉及代數式的比較時,還要適當的使用分類討論法)
綜合運用
解題步驟
(1) 求出每個不等式的
解集;
 一元一次不等式
一元一次不等式(2) 求出每個不等式的解集的公共部分;(一般利用
數軸)
(3) 用
代數符號語言來表示公共部分。(也可以說成是聲明
結論)
常見解法
(1) 關於x不等式組{x>a} {x>b}的
解集是:
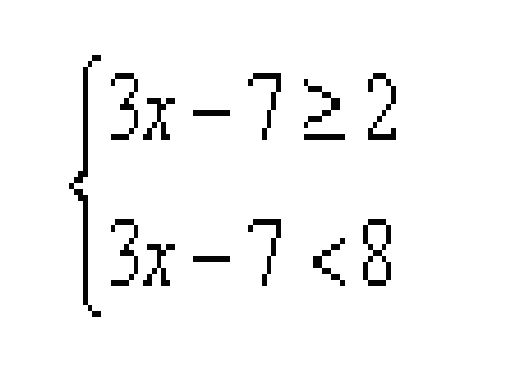 一元一次不等式組
一元一次不等式組(2) 關於x不等式組{x<a} {x<b}的
解集是:
(3) 關於x不等式組{x>a} {x<b}的解集是:
(4) 關於x不等式組{x<a} {x>b}的
解集是
空集。
以上取解集的方法可歸納為:兩大取大,兩小取小,大小小大取中間,大大小小無解
特殊不等式組解
(1) 關於x
不等式(組):{x≥a} { x≤a}的
解集為:
 一元一次不等式與一次函式取值域之間的聯繫
一元一次不等式與一次函式取值域之間的聯繫與一元一次方程
不同點:一元一次不等式表示不等關係,
一元一次方程表示
相等關係;一個是運用等式的基本性質,另一個則是不等式的基本性質。
相同點:二者都是只含有一個
未知數,未知數的次數都是1,左右兩邊都是
整式。一般步驟都是:去分母;去括弧;移項;合併同類項;將未知數的係數化為1。
例題解析
例3 解下列不等式
(1) 2x-1<4x+13;
(2)(5x+3)≤x-3(1-2x)
解 (1)2x-1<4x+13,
2x-4x<13+1,
-2x<14,
x>-7。
(2)2(5x+3)≤x-3(1-2x),
10x+6≤x-3+6x,
3x≤-9,
x≤-3。
試題列舉
1、一本英語書98頁,孟濤讀了7天(一周)還沒讀完,而張浩不到一周就讀完了,張浩平均每天比孟濤多讀3頁,問孟濤每天讀多少頁?
解:設孟濤每天讀x頁,則張浩讀(x+3)頁,由題意,得:
{98/x>7
{98/(x+3)<7
解得:11<x<14
∴孟濤每天讀12或13頁
∴x+3=15或16頁
∴張浩每天讀15或16頁
2、把一些書分給幾個學生,如果每人分3本,那么餘8本;如果前面的每個學生分5本,那么最後一人就分不到3本。問這些書有多少本?學生有多少人?
解:設學生有x人 ,由題意,得:
{3x+8-5(x-1)≥0
{3x+8-5(x-1)<3
解得:5<x≤6
∵由於學生的數量x只能取整數,不為小數。
∴x=6
∴書本有:3×6+8=26(本)
3、用每分鐘抽1.1噸水的A型抽水機來抽池水,半小時可以抽完;如果改用B型抽水機,估計20分鐘到22分可以抽完。B型抽水機比A型抽水機每分鐘約多抽多少噸水?
解:設B型每分鐘抽x噸,由題意,得:
{20x≤1.1*30
{22x≥1.1*30
解得:1.5≤x≤1.65
∴1.5-1.1≤x-1.1≤1.65-1.1
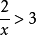
 一元一次不等式
一元一次不等式

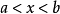

 用數軸法解一元一次不等式
用數軸法解一元一次不等式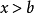
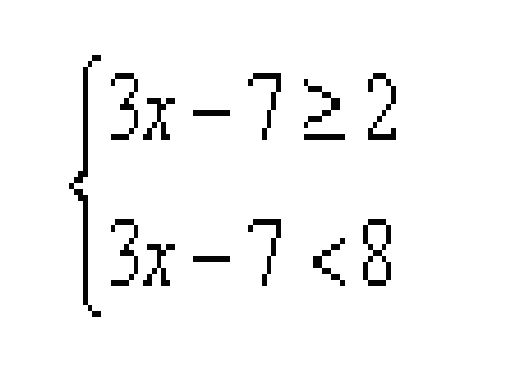 一元一次不等式組
一元一次不等式組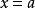
 一元一次不等式與一次函式取值域之間的聯繫
一元一次不等式與一次函式取值域之間的聯繫