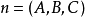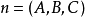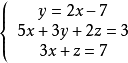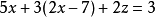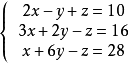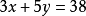定義
含有3個未知數,並且含有未知數的項的次數都是1的
整式方程叫做三元一次方程,可化為一般形式ax+by+cz=d(a、b、c≠0)或ax+by+cz+d=0(a、b、c≠0)。
三元一次方程的解
適合一個三元一次方程的每一對未知數的值,叫做這個三元一次方程的一個解。對於任何一個三元一次方程,令其中兩個未知數取任意兩個值,都能求出與它對應的另一個未知數的值。因此,任何一個三元一次方程都有無數多個解,由這些解組成的集合,叫做這個三元一次方程的解集。
...
與空間平面
數學課程 中的方程與空間幾何圖形比如平面、曲面、直線、曲線是有對應關係的,三元一次方程就與空間幾何圖形——空間平面相對應。 一些特殊的三元一次方程,比如常數項為零、或者只含有兩個未知數 、或者只含有一個未知數的就會與一些特殊的空間平面相對應。
已知平面上的一點
和它的一個法線向量
, 對平面上的任一 點
,有向量
,
。由空間兩個向量垂直的充要條件有,
,代入坐標有:
上式為空間平面的點法式方程。注意到該方程是
的一次方程,故可推定 :任一平面都可以用三元一次方程來表示。這是因為任一平面都可以由它的法向量與它上面的一點唯一決定,而平面的點法式方程本身就是三元一次方程。
反過來,若有三元一次方程
兩式相減,得:
,該方程是過點
且以
為法向量的平面方程。由此可知,三元一次方程所代表的圖形是平面。
三元一次方程組
定義
由多個一元一次方程組成並含有三個未知數的方程組叫做三元一次方程組
注意:每個方程不一定都含有三個未知數,但方程組整體上要含有三個未知數。
求解思路
解三元一次方程組的基本思想仍是消元,其基本方法是代入消元法和加減消元法。
步驟:
①利用代入法或加減法,消去一個未知數,得到一個二元一次方程組;
②解這個二元一次方程組,求得兩個未知數的值;
③將這兩個未知數的值代入原方程中含有三個未知數的一個方程,求出第三個未知數的值,把這三個未知數的值用一個大括弧寫在一起就是所求的三元一次方程組的解。
舉例
例1
解:
對方程組中得方程進行標號
對方程組進行分析:該方程組可用代入法先消去y,把①代入②,得,
例2
解:
對方程組進行標號,
對方程組進行分析:從三個方程的未知數的係數特點來考慮,先消z比較簡單。
④與⑤組成一個二元一次方程組,解這個方程組,得 x、y值;把x、y值方程③,得z值。
注意:為把三元一次方程組轉化為二元一次方程組,原方程組中的每個方程至少要用一次。