二元一次不等式是指含有兩個未知數(即二元),並且未知數的次數是1次(即一次)的不等式。
滿足二元一次不等式(組)的x和y的取值構成有序數對(x，y)，所有這樣的有序數對(x，y)構成的集合稱為二元一次不等式(組)的解集。
基本介紹
- 中文名：二元一次不等式
- 外文名：linear inequation in two unknowns
- 學科：數理科學
- 類型：數學術語
- 特點：含有兩個未知數且次數是1次
- 屬於：不等式
不等式,簡介,解集,表示平面區域,二元一次不等式組,例題,
不等式
一般地，用純粹的大於號“>”、小於號“<”連線的不等式稱為嚴格不等式，用不小於號（大於或等於號）“≥”、不大於號（小於或等於號）“≤”連線的不等式稱為非嚴格不等式，或稱廣義不等式。總的來說，用不等號(<,>,≥,≤,≠)連線的式子叫做不等式。
其中，兩邊的解析式的公共定義域稱為不等式的定義域。
整式不等式：
整式不等式兩邊都是整式（即未知數不在分母上）。
一元一次不等式：含有一個未知數(即一元)，並且未知數的次數是1次(即一次)的不等式。如3-X>0。
簡介
二元一次不等式是指含有兩個未知數(即二元)，並且未知數的次數是1次(即一次)的不等式。
解集
一般地， 在直角坐標系中，二元一次不等式表示某側所有點組成的平面區域。我們把直線畫成虛線時，表示區域不包括邊界。而不等式表示區域包括邊界時，則把邊界畫成實線：不等式組表示的平面區域是各個不等式所表示的平麵點集的交集，因而是各個不等式所表示的平面區域的公共部分。
直線與二元一次方程
直線與二元一次方程表示平面區域
在教學中發現，由直線方程一般式的係數特徵，可判斷直線位置關係的方法，類比可得到由二元一次不等式Ax+By+C > 0的係數特徵(A，B的符號特徵)，確定二元一次不等式ax+By+c > 0表示的平面區域的規律，下面給予介紹，以供參考。
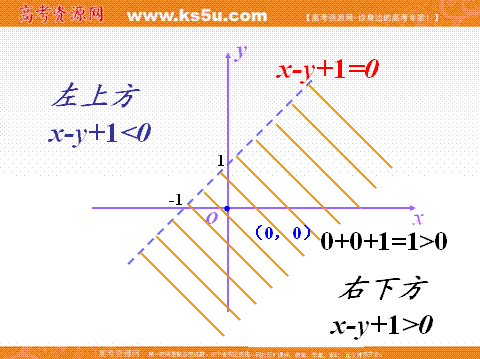
（1）若A>0，B>0，則二元一次不等式ax+By+C > 0表示直線Az+By+C=0右上方的平面區域；
（2） A>0，B<0時，二元一次不等式Ax+ By+C >0表示直線Ax十By十C=0右下方的平面區域；
（3）A<0，B>0時，二元一次不等式Ax+By+C > 0表示直線Ax十By+C=0左上方的平面區域；
（4） A<0，B<0時，二元一次不等式Ax+ By+C > 0表示直線Ax+By+c=0左下方的平面區域；
（5）A=0，B>0時，二元一次不等式Ax+ By+C> 0表示直線
上方的平面區域；
（6）A=0，B<0時，二元一次不等式Ax+ By+C> 0表示直線下方的平面區域；
（7）A>0，B=0時，二元一次不等式Ax+ By+C> 0表示直線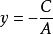
右側的平面區域；
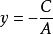
（8）A<0，B=0時，二元一次不等式Ax+ By+C>0表示直線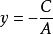左側的平面區域。
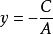
二元一次不等式組
一般地，關於兩個未知數的幾個二元一次不等式合在一起，就組成一個二元一次不等式組。
用加減法解不等式的時候，不用去記住很多代入法要注意的小技巧，特別是考試時比較緊張，如果要記住太多很容易出錯的。這種相加法，用熟之後過程可以不用這么繁複，可以少寫一兩步。
特別注意，根據不等式性質，不等號方向相同的兩式子，只能相加，不能相減。
不等號方向相反時，兩邊才能相減，相減後的不等號方向與被減式相同。實際這跟兩式相加一樣的，只要把式子兩邊交換，">號"會變"<"號。不過這方法不嚴謹，只能用於選擇填空，用於做大題會被判錯的。而且比兩式相加容易出錯，所以一開始就乖乖做兩式相加好了，等熟練了以後，做選擇填空才用兩式相減。
舉例，2x+y>10……①
x+y<5………②
①-②，不等號取> 可理解為：①+（-②）
(2x+y)-(x+y)>10-5
得x>5
將x>5帶入②得，y<0
例題
A判斷下列句子是否正確。
(a)若 2x> –12，則x> –6。
(b)若x+11>0 ，則x> –11。
(c)若 a< 2 < b，則(a– 2)(b– 2) < 0。
(d)若 a> b及 c> d，則a– c> b– d。
(e)若 a> b，則a– 4 > b– 4。
(f)若 a> 0 > b，則a> b。
答案：a對；b對；c對；d錯；e對；f對；
B 在3x-y+5>0表示的直線y=3x+5上方還是下方區域？
答：A>0，B<0時，二元一次不等式Ax+ By+C >0表示直線Ax十By十C=0右下方的平面區域，此時A=3>0，B=-1<0，所以是下方區域。
