基本介紹
- 中文名:整式不等式
- 外文名:inequality of integral expression
- 所屬學科:數學
- 所屬問題:初等代數(不等式)
- 性質:一種有理不等式
基本介紹

整式不等式的解法



















例題解析

 圖1
圖1
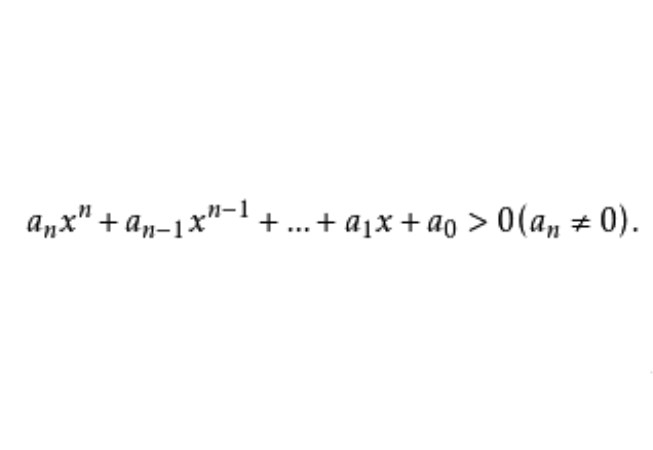





















 圖1
圖1
整式不等式(inequality of integral expression)是一種有理不等式,指不等式的兩端都是整式者,整式不等式按未知數的個數和不等式的次數分類,含有n個未知數,且兩端...
一般地,用純粹的大於號“>”、小於號“<”連線的不等式稱為嚴格不等式,用不小於號(大於或等於號)“≥”、不大於號(小於或等於號)“≤”連線的不等式稱為非...
一次不等式(linear inequality)是一種整式不等式,若整式不等式的次數為1,則稱為一次不等式。一次不等式中若含有n個未知數,則稱為n元一次不等式。...
與分式方程類似,像f(x)/g(x)>0或f(x)/g(x)<0(其中f(x)、g(x)為整式且g(x)不為0)這樣,分母中含有未知數的不等式稱為分式不等式(fractional ...
一元一次不等式是一個數學算式,類似於一元一次方程,含有一個未知數,未知數的次數是1,未知數的係數不為0,左右兩邊為整式的不等式,叫做一元一次不等式。...
有理不等式(rational inequality)一種代數不等式.指用不等號連結兩個有理式所成的表達式。...
含有等號的式子叫做等式。等式可分為矛盾等式和條件等式。等式兩邊同時加上(或減去)同一個整式,或者等式兩邊同時乘或除以同一個不為0的整式,等式仍然成立。形式是...
不等式是用不等號將兩個解析式連結起來所成的式子。在一個式子中的數的關係,不全是等號,含不等符號的式子,那它就是一個不等式。例如2x+2y≥2xy,sinx≤1,...
對數不等式是一種兩邊由對數構成的不等式。...... 第(2)問是含參分式不等式的解法,先要等價轉化為整式不等式,再就兩根與2的大小分三種情況討論. </t</x</...
一元分式不等式(fractional inequality in one unknown)是一種常見的分式不等式,指含有一個未知數的分式不等式。設f(x),g(x)有一個是分式,另一個是分式或...
一般地,用純粹的大於號“>”、小於號“<”連線的不等式稱為嚴格不等式,用不小於號(大於或等於號)“≥”、不大於號(小於或等於號)“≤”連線的不等式稱為非...
4.2整式與方程(組)、不等式(組)的綜合問題 4.2.1整式與方程(組)的綜合問題 4.2.2整式與不等式(組)的綜合問題 4.3整式的套用參考...
當高次不等式f(x)>0(或<0)的左邊整式、分式不等式φ(x)/h(x)>0(或<0)的左邊分子、分母能分解成若干個一次因式的積(x-a1)(x-a2)…(x-an)的形式,...
基本性質2:不等式兩邊同時乘以(或除以)同一個大於0的整式,不等號方向不變基本性質3:不等式兩邊同時乘以(或除以)同一個小於0的整式,不等號方向改變...
