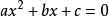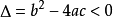一元二次不等式,是指含有一個未知數且未知數的最高次數為2的不等式叫做一元二次不等式。它的一般形式是 ax2+bx+c>0 、ax2+bx+c≠0、ax2+bx+c<0(a不等於0)。
基本介紹
- 中文名:一元二次不等式
- 外文名:One-Variable Quadratic inequality
- 一般形式: ax2+bx+c>0 或 ax2+bx+c<0
- 類型:不等式
- 未知數:一個未知數且最高次數為2
- 歸屬學科:數學
一般形式,求解方法,解法一,解法二,解法三,解法四,判別方法,
一般形式
形如 (或
(或 )(其中,
)(其中, )這樣,只含有一個未知數,並且未知數的最高次數是2的不等式,稱為關於
)這樣,只含有一個未知數,並且未知數的最高次數是2的不等式,稱為關於 的一元二次不等式。
的一元二次不等式。




求解方法
解法一
當 時,一元二次方程
時,一元二次方程 無實根。
無實根。


舉例:
試解一元二次不等式

解:
然後,分兩種情況討論。
1)

得 且
且 (不成立)
(不成立)


2)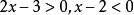
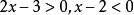
得 且
且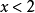 。
。

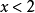
得最終不等式的解為:

解法二
可利用用配方法解一元二次不等式。
如上面例題中,採用配方法求解如下:



故原不等式 可化為:
可化為:


於是有:

故不等式的解集為

解法三
一元二次不等式也可通過一元二次函式圖象進行求解。
通過看圖象可知,二次函式圖象與X軸的兩個交點,然後根據題中所需求"<0"或">0"而推出答案。
求一元二次不等式的解集實際上是將這個一元二次不等式的所有項移到不等式一側並進行因式分解分類討論求出解集。解一元二次不等式,可將一元二次方程不等式轉化成二次函式的形式,求出函式與X軸的交點,將一元二次不等式,二次函式,一元二次方程聯繫起來,並利用圖象法進行解題,使得問題簡化。
 圖1方程、不等式和其解集的關係
圖1方程、不等式和其解集的關係解法四
數軸穿根:用穿根法解高次不等式時,就是先把不等式一端化為零,再對另一端分解因式,並求出它的零點,把這些零點標在數軸上,再用一條光滑的曲線,從x軸的右端上方起,依次穿過這些零點,大於零的不等式的解對應這曲線在 軸上方部分的實數
軸上方部分的實數 的值的集合,小於零的則相反。這種方法叫做序軸穿根法,又叫“穿根法”。口訣是“從右到左,從上到下,奇穿偶不穿。”
的值的集合,小於零的則相反。這種方法叫做序軸穿根法,又叫“穿根法”。口訣是“從右到左,從上到下,奇穿偶不穿。”


註:該方法適用於所有的不等式。
步驟:
1)把二次項係數變成正的;
2)畫數軸,在數軸上從小到大依次標出所有根;
3)從右上角開始,一上一下依次穿過不等式的根,奇過偶不過(即遇到含 的項是奇次冪就穿過,偶次冪就跨過);
的項是奇次冪就穿過,偶次冪就跨過);

4)注意看看題中不等號有沒有等號,沒有的話還要注意捨去使不等式為 的根。
的根。

舉例:
解不等式:

解:
1)將最高次項係數化為正,這裡本就是正的,便無需轉化;
2)分解因式,得: ;
;

3)找方程 的根:
的根: 或
或 ;
;



3)畫數軸,並把根所在的點標上去;
4)注意,此時從最右端開始,從2的右上方引出一條曲線,經過點2,繼續向左繪製,類似於拋物線,再經過點1,向點1的左上方無限延伸;
5)題中要求 的解,那么只需在數軸上觀察哪一段在數軸及數軸以下即可,觀察可以得到:
的解,那么只需在數軸上觀察哪一段在數軸及數軸以下即可,觀察可以得到: 。
。


註:高次不等式亦如此,例如一個分解因式後所得之不等式:

先找方程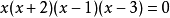 的根:
的根:
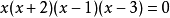

在數軸上依次標出這些點。還是從最右邊的一點3的右上方引出一條曲線,經過點3,在1、3之間類似於一個開口向上的拋物線,經過點1;繼續向點1的左上方延伸,這條曲線在點0、1之間類似於一條開口向下的曲線,經過點0;繼續向0的左下方延伸,在0、-2之間類似於一條開口向上的拋物線,經過點-2;繼續向點-2的左上方無限延伸。
由於方程中要求的是>0,只需觀察曲線在數軸上方的部分所取的x的範圍即可,故為: 或
或 或
或 。
。



該方法需注意的是:
1)遇到根是分數或無理數和遇到整數時的處理方法是一樣的,都是在數軸上把這個根的位置標出來;
2)“奇過偶不過”中的“奇、偶”指的是分解因式後。某個因數的指數是奇數或者偶數;比如不等式 ,
, 的指數是2,是偶數,所以在數軸上畫曲線時就不穿過2這個點;而
的指數是2,是偶數,所以在數軸上畫曲線時就不穿過2這個點;而 的指數是1,是奇數,所以在數軸上畫曲線時就要穿過3這個點。
的指數是1,是奇數,所以在數軸上畫曲線時就要穿過3這個點。



3)分子中一定都是能夠因式分解成一次式的因式,否則不能用此方法。
判別方法
1)當  時:
時:

2)當 時:
時: