統計學(一級學科)

統計學是通過搜尋、整理、分析、描述數據等手段，以達到推斷所測對象的本質，甚至預測對象未來的一門綜合性科學。統計學用到了大量的數學及其它學科的專業知識，其套用範圍幾乎覆蓋了社會科學和自然科學的各個領域。

基本介紹

• 中文名：統計學
• 外文名：Statistics
• 學科門類：一級學科
• 學科特點：套用廣泛
• 主要分支：社會統計學、數理統計學 

發展過程

起源

統計學的英文statistics最早源於現代拉丁文Statisticum Collegium（國會）、義大利文Statista（國民或政治家）以及德文Statistik，最早是由Gottfried Achenwall於1749年使用，代表對國家的資料進行分析的學問，也就是“研究國家的科學”。十九世紀，統計學在廣泛的數據以及資料中探究其意義，並且由John Sinclair引進到英語世界。

統計在金融上套用廣泛

統計學是一門很古老的科學，一般認為其學理研究始於古希臘的亞里士多德時代，迄今已有兩千三百多年的歷史。它起源於研究社會經濟問題，在兩千多年的發展過程中，統計學至少經歷了“城邦政情”、“政治算數”和“統計分析科學”三個發展階段。所謂“數理統計”並非獨立於統計學的新學科，確切地說，它是統計學在第三個發展階段所形成的所有收集和分析數據的新方法的一個綜合性名詞。機率論是數理統計方法的理論基礎，但是它不屬於統計學的範疇，而是屬於數學的範疇。

城邦政情

“城邦政情”（Matters of state）階段始於古希臘的亞里斯多德撰寫“城邦政情”或“城邦紀要”。他一共撰寫了一百五十餘種紀要，其內容包括各城邦的歷史、行政、科學、藝術、人口、資源和財富等社會和經濟情況的比較、分析，具有社會科學特點。“城邦政情”式的統計研究延續了一兩千年，直至十七世紀中葉才逐漸被“政治算術”這個名詞所替代，並且很快被演化為“統計學”（Statistics）。但統計學依然保留了城邦（state）這個詞根。

政治算術

與“城邦政情”階段沒有很明顯的分界點，本質的差別也不大。

威廉·配第

“政治算術”的特點是統計方法與數學計算和推理方法開始結合。分析社會經濟問題的方式更加注重運用定量分析方法。

1690年英國威廉·配弟出版《政治算數》一書作為這個階段的起始標誌。

威廉·配第用數字、重量和尺度將社會經濟現象數量化的方法是近代統計學的重要特徵。因此，威廉·配第的《政治算術》被後來的學者評價為近代統計學的來源，威廉·配第本人也被評價為近代統計學之父。

配第在書中使用的數字有三類：

第一類是對社會經濟現象進行統計調查和經驗觀察得到的數字。因為受歷史條件的限制，書中通過嚴格的統計調查得到的數據少，根據經驗得出的數字多；

第二類是運用某種數學方法推算出來的數字。其推算方法可分為三種：

(1)以已知數或已知量為基礎，循著某種具體關係進行推算的方法；

(2)通過運用數字的理論性推理來進行推算的方法；

(3)以平均數為基礎進行推算的方法”；

第三類是為了進行理論性推理而採用的例示性的數字。配第把這種運用數字和符號進行的推理稱之為“代數的算法”。從配第使用數據的方法看，“政治算數”階段的統計學已經比較明顯地體現了“收集和分析數據的科學和藝術”特點，統計實證方法和理論分析方法渾然一體，這種方法即使是現代統計學也依然繼承。

統計分析科學

在“政治算術”階段出現的統計與數學的結合趨勢逐漸發展形成了“統計分析科學”。

十九世紀末，歐洲大學開設的“國情紀要”或“政治算數”等課程名稱逐漸消失，代之而起的是“統計分析科學”課程。當時的“統計分析科學”（Science of statistical analysis）課程的內容仍然是分析研究社會經濟問題。

“統計分析科學”課程的出現是現代統計發展階段的開端。1908年，“學生”氏（William Sleey Gosset的筆名Student）發表了關於t分布的論文。這是一篇在統計學發展史上劃時代的文章，它創立了小樣本代替大樣本的方法，開創了統計學的新紀元。

現代統計學的代表人物首推比利時統計學家奎特萊（Adolphe Quelet），他將統計分析科學廣泛套用於社會科學，自然科學和工程技術科學領域，因為他深信統計學是可以用於研究任何科學的一般研究方法.

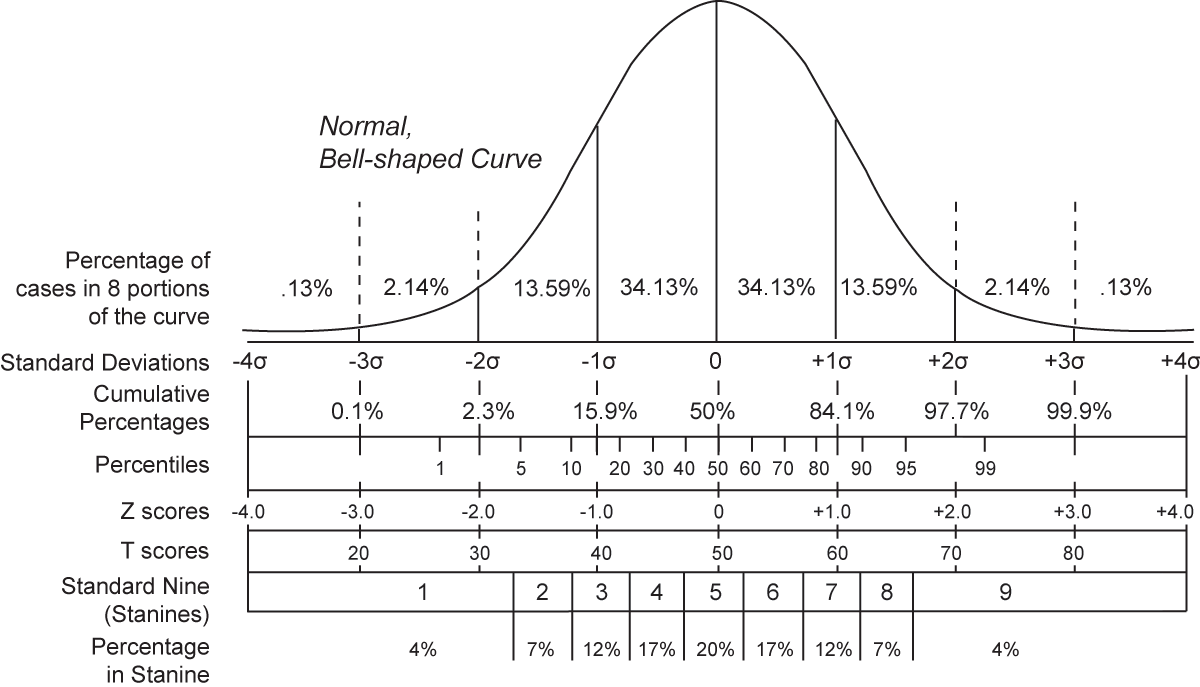
常態分配的鐘型曲線

現代統計學的理論基礎機率論始於研究賭博的機遇問題，大約開始於1477年。數學家為了解釋支配機遇的一般法則進行了長期的研究，逐漸形成了機率論理論框架。在機率論進一步發展的基礎上，到十九世紀初，數學家們逐漸建立了觀察誤差理論，常態分配理論和最小平方法則。於是，現代統計方法便有了比較堅實的理論基礎。

主要術語

統計學（statistics）：收集、處理、分析、解釋數據並從數據中得出結論的科學。

描述統計（descriptive statistics）：研究數據收集、處理和描述的統計學方法。

推斷統計（inferential statistics）：研究如何利用樣本數據來推斷總體特徵的統計學方法。

變數（variable）：統計上的絕對量指標，按連續性分可分為離散變數與連續變數。按性質分可分為確定性變數和隨機變數。

分類變數（categorical variable）：觀測結果表現為某種類別的變數。

順序變數（rank variable）：又稱有序分類變數，觀測結果表現為某種有序類別的變數。

數值型變數（metric variable）：又稱定量變數，觀測結果表現為數字的變數。

均值（mean）：均值也就是平均數，有時特指算術平均數，這是相對其他方式計算的均值，求法是先將所有數字加起來，然後除以數字的個數，這是測量集中趨勢，或者說平均數的一種方法。

中位數（median）：又稱中值，是按順序排列的一組數據中居於中間位置的數，其可將數值集合劃分為相等的上下兩部分。

眾數（mode）：眾數也就是數據集中出現頻率最多的數字。

相關觀念

統計中的各種圖

為了將統計學套用到科學，工業以及社會問題上，我們由研究母體開始。這可能是一個國家的人民，石頭中的水晶，或者是某家特定工廠所生產的商品。一個母體甚至可能由許多次同樣的觀察程式所組成；由這種資料收集所組成的母體我們稱它叫時間序列。

為了實際的理由，我們選擇研究母體的子集代替研究母體的每一筆資料，這個子集稱做樣本。以某種經驗設計實驗所蒐集的樣本叫做資料。資料是統計分析的對象，並且被用做兩種相關的用途：描述和推論。描述統計學處理有關敘述的問題：資料是否可以通過以數學或是圖片形式來被有效的摘要以用來代表母體的性質？基礎的數學描述包括了平均數和標準差。圖像的摘要則包含了許多種的表和圖。

推論統計學被用來將資料中的數據模型化，計算它的機率並且做出對於母體的推論。這個推論可能以對/錯問題的答案所呈現（假設檢定），對於數字特徵量的估計（估計），對於未來觀察的預測，關聯性的預測（相關性），或是將關係模型化（回歸）。其他的模型化技術包括變異數分析（ANOVA），時間序列，以及數據挖掘。

相關的觀念特別值得被拿出來討論。對於資料集合的統計分析可能顯示兩個變數（母體中的兩種性質）傾向於一起變動，好像它們是相連的一樣。舉例來說，對於人收入和死亡年齡的研究期刊可能會發現窮人比起富人平均來說傾向擁有較短的生命。這兩個變數被稱做相關的。但是實際上，我們不能直接推論這兩個變數中有因果關係；參見相關性推論因果關係（邏輯謬誤）。

如果樣本足以代表母體的，那么由樣本所做的推論和結論可以被引申到整個母體之上。最大的問題在於決定樣本是否足以代表 整個母體。統計學提供了許多方法來估計和修正樣本和收集資料過程中的隨機性（誤差），如同上面所提到的透過經驗所設計的實驗。參見實驗設計。

要了解隨機性或是機率必須具備基本的數學觀念。數理統計（通常又叫做統計理論）是套用數學的分支，它使用機率論來分析並且驗證統計的理論基礎。

任何統計方法是有效的只有當這個系統或是所討論的母體滿足方法論的基本假設。誤用統計學可能會導致描述面或是推論面嚴重的錯誤，這個錯誤可能會影響社會政策，醫療實踐以及橋樑或是核能發電計畫結構的可靠性。

即使統計學被正確的套用，結果對於不是專家的人來說可能會難以陳述。舉例來說，統計資料中顯著的改變可能是由樣本的隨機變數所導致，但是這個顯著性可能與大眾的直覺相悖。人們需要一些統計的技巧（或懷疑）以面對每天日常生活中透過引用統計數據所獲得的資訊。

統計方法

測量的尺度

統計學一共有四種測量的尺度或是四種測量的方式。這四種測量（名目、順序、等距、等比）在統計過程中具有不等的實用性 。

等比尺度（Ratio measurements）擁有零值及資料間的距離是相等被定義的；

等距尺度（Interval measurements）資料間的距離是相等被定義的但是它的零值並非絕對的無而是自行定義的（如智力或溫度的測量）；

順序尺度（ Ordinal measurements）的意義並非表現在其值而是在其順序之上；

名目尺度（Nominal measurements）的測量值則不具量的意義。

統計技術

以下列出一些有名的統計檢定方法以及可供驗證實驗數據的程式

英國統計學家費希爾

Fisher最小顯著差異法（Fisher's Least Significant Difference test ）

學生t檢驗（Student's t-test）

曼-惠特尼 U 檢定（Mann-Whitney U）

回歸分析（regression analysis）

相關性（correlation）

皮爾森積矩相關係數（Pearson product-moment correlation coefficient）

史匹曼等級相關係數（Spearman's rank correlation coefficient ）

卡方分布（chi-square ）

創立時期

德國的斯勒茲曾說過：“統計是動態的歷史，歷史是靜態的統計”。可見統計學的產生與發展是和生產的發展、社會的進步緊密相聯的。

統計學的萌芽產生在歐洲，17世紀中葉至18世紀中葉是統計學的創立時期。在這一時期，統計學理論初步形成了一定的學術派別，主要有國勢學派和政治算術學派。

國勢學派

統計學的萌芽最初在當時歐洲經濟發展較快的義大利孕育良久，但最終卻在17世紀的德國首先破土成芽，國勢學派又稱記述學派，產生於17世紀的德國。由於該學派主要以文字記述國家的顯著事項，故稱記述學派。其主要代表人物是海爾曼·康令和阿亨華爾。康令第一個在德國黑爾姆斯太特大學以“國勢學”為題講授政治活動家應具備的知識。阿亨華爾在哥廷根大學開設“國家學”課程，其主要著作是《近代歐洲各國國勢學綱要》，書中講述“一國或多數國家的顯著事項”，主要用對比分析的方法研究了解國家組織、領土、人口、資源財富和國情國力，比較了各國實力的強弱，為德國的君主政體服務。因在外文中“國勢”與“統計”詞義相通，後來正式命名為“統計學”。該學派在進行國勢比較分析中，偏重事物性質的解釋，而不注重數量對比和數量計算，但卻為統計學的發展奠定了經濟理論基礎。但隨著經濟的發展，對事物量的計算和分析顯得越來越重要，該學派後來發生了分裂，分化為圖表學派和比較學派。

德國格廷根大學

德國經濟學家稱阿亨瓦爾為“統計學之父”, 但英國學者有爭議, 聲稱阿亨瓦爾忽略了威廉·配第(William Petty, 1623-1687)的和其他學者的主張。威廉·配第的《政治算術》(1676)中用數字、重量和尺度將社會經濟現象數量化的方法是近代統計學的重要特徵，因此威廉·配第是近代統計學之父。

政治算術學派

政治算術學派產生於17世紀中葉的英國，創始人是威廉·配第（1623-1687），其代表作是他於1676年完成的《政治算術》一書。這裡的“政治”是指政治經濟學，“算術”是指統計方法。在這部書中，他利用實際資料，運用數字、重量和尺度等統計方法對英國、法國和荷蘭三國的國情國力，作了系統的數量對比分析，從而為統計學的形成和發展奠定了方法論基礎。因此馬克思說：“威廉·佩第——政治經濟學之父，在某種程度上也是統計學的創始人”。

政治算術學派的另一個代表人物是約翰·格朗特（1620-1674）。他以1604年倫敦教會每周一次發表的“死亡公報”為研究資料，在 1662年發表了《關於死亡公報的自然和政治觀察》的論著。書中分析了60年間倫敦居民死亡的原因及人口變動的關係，首次提出通過大量觀察，可以發現新生兒性別比例具有穩定性和不同死因的比例等人口規律；並且第一次編制了“生命表”，對死亡率與人口壽命作了分析，從而引起了普遍的關注。他的研究清楚地表明了統計學作為國家管理工具的重要作用。

發展時期

18世紀末至19世紀末是統計學的發展時期。在這一時期，各種學派的學術觀點已經形成，並且形成了兩個主要學派，即數理統計學派和社會統計學派。

數理統計學派

在18世紀，由於機率理論日益成熟，為統計學的發展奠定了基礎。19世紀中葉，把機率論引進統計學而形成數理學派。其奠基人是比利時的阿道夫·凱特勒（1796-1874），其主要著作有：《論人類》、《機率論書簡》、《社會制度》和《社會物理學》等。他主張用研究自然科學的方法研究社會現象，正式把古典機率論引進統計學，使統計學進入一個新的發展階段。由於歷史的局限性，凱特勒在研究過程中混淆了自然現象和本質區別，對犯罪、道德等社會問題，用研究自然現象的觀點和方法作出一些機械的、庸俗化的解釋。但是，他把機率論引入統計學，使統計學在“政治算術”所建立的“算術”方法的基礎上，在準確化道路上大大跨進了一步，為數理統計學的形成與發展奠定了基礎。

阿道夫·凱特勒

社會統計學派

產生於19世紀後半葉，創始人是德國經濟學家、統計學家克尼斯（1821-1889），主要代表人物主要有恩格爾（1821- 1896）、梅爾（1841-1925）等人。他們融合了國勢學派與政治算術學派的觀點，沿著凱特勒的“基本統計理論”向前發展，但在學科性質上認為統計學是一門社會科學，是研究社會現象變動原因和規律性的實質性科學，以此同數理統計學派通用方法相對立。社會統計學派在研究對象上認為統計學是研究體而不是個別現象，而且認為由於社會現象的複雜性和整體性，必須地總體進行大量觀察和分析，研究其內在聯繫，才能揭示現象內在規律。這是社會統計學派的“實質性科學”的顯著特點。

恩斯特·恩格爾

社會經濟的發展，要求統計學提供更多的統計方法；社會科學本身也不斷地向細分化和定量化發展，也要求統計學能提供更有效的調查整理、分析資料的方法。因此，社會統計學派也日益重視方法論的研究，出現了從實質性方法論轉化的趨勢。但是，社會統計學派仍然強調在統計研究中必須以事物的質為前提和認識事物質的重要性，這同數理統計學派的計量不計質的方法論性質是有本質區別的。

迅速發展

現代

20世紀初以來，科學技術迅猛發展，社會發生了巨大變化，統計學進入了快速發展時期。歸納起來有以下幾個方面。

1、由記述統計向推斷統計發展。記述統計是對所蒐集的大量數據資料進行加工整理、綜合概括，通過圖示、列表和數字，如編制次數分布表、繪製直方圖、計算各種特徵數等，對資料進行分析和描述。而推斷統計，則是在蒐集、整理觀測的樣本數據基礎上，對有關總體作出推斷。其特點是根據帶隨機性的觀測樣本數據以及問題的條件和假定（模型），而對未知事物作出的，以機率形式表述的推斷。當今西方國家所指的科學統計方法，主要就是指推斷統計來說的。

2、由社會、經濟統計向多分支學科發展。在20世紀以前，統計學的領域主要是人口統計、生命統計、社會統計和經濟統計。隨著社會、經濟和科學技術的發展，到今天，統計的範疇已覆蓋了社會生活的一切領域，幾乎無所不包，成為通用的方法論科學。它被廣泛用於研究社會和自然界的各個方面，並發展成為有著許多分支學科的科學。

3、統計預測和決策科學的發展。傳統的統計是對已經發生和正在發生的事物進行統計，提供統計資料和數據。20世紀30年代以來，特別是第二次世界大戰以來，由於經濟、社會、軍事等方面的客觀需要，統計預測和統計決策科學有了很大發展，使統計走出了傳統的領域而被賦予新的意義和使命。

當代現狀

資訊理論、控制論、系統論與統計學的相互滲透和結合，使統計科學進一步得到發展和日趨完善。資訊理論、控制論、系統論在許多基本概念、基本思想、基本方法等方面有著共同之處，三者從不同角度、側面提出了解決共同問題的方法和原則。三論的創立和發展，徹底改變了世界的科學圖景和科學家的思維方式，也使統計科學和統計工作從中吸取了營養，拓寬了視野，豐富了內容，出現了新的發展趨勢。

資訊理論創始人香農

計算技術和一系列新技術、新方法在統計領域不斷得到開發和套用。近幾十年間，計算機技術不斷發展，使統計數據的蒐集、處理、分析、存貯、傳遞、印製等過程日益現代化，提高了統計工作的效能。計算機技術的發展，日益擴大了傳統的和先進的統計技術的套用領域，促使統計科學和統計工作發生了革命性的變化。如今，計算機科學已經成為統計科學不可分割組成部分。隨著科學技術的發展，統計理論和實踐深度和廣度方面也不斷發展。

統計在現代化管理和社會生活中的地位日益重要。隨著社會、經濟和科學技術的發展，統計在現代化國家管理和企業管理中的地位，在社會生活中的地位，越來越重要了。人們的日常生活和一切社會生活都離不開統計。英國統計學家哈斯利特說：“統計方法的套用是這樣普遍，在我們的生活和習慣中，統計的影響是這樣巨大，以致統計的重要性無論怎樣強調也不過分”。甚至有的科學家還把我們的時代叫做“統計時代”。顯然，20世紀統計科學的發展及其未來，已經被賦予了劃時代的意義。

高校排名

第四輪學科評估高校排名：0714 統計學

第四輪學科評估於2016年4月啟動，按照“自願申請、免費參評”原則，採用“客觀評價與主觀評價相結合”的方式進行。評估體系在前三輪的基礎上進行諸多創新；評估數據以“公共數據和單位填報相結合”的方式獲取；評估結果按“分檔”方式呈現，具體方法是按“學科整體水平得分”的位次百分位，將前70%的學科分9檔公布：前2%（或前2名）為A+，2%～5%為A（不含2%，下同），5%～10%為A-，10%～20%為B+，20%～30%為B，30%～40%為B-，40%～50%為C+，50%～60%為C，60%～70%為C-。

本一級學科中，全國具有“博士授權”的高校共54所，本次參評51所；部分具有“碩士授權”的高校也參加了評估；參評高校總計120所。

還有一個科研機構參加了該學科的評估

14430

中國科學院大學

A-

分支學科

主分支

統計學史

理論統計學統計調查分析理論

《統計學——科學與工程套用》封面圖

統計核算理論

統計監督理論

統計預測理論

統計邏輯學

統計法學

描述統計學

推斷統計學

經濟統計學

巨觀經濟統計學

微觀經濟統計學

管理統計學

科學技術統計學

農村經濟調查

社會統計學

教育統計學

文化與體育統計學

衛生統計學

司法統計學

社會福利與社會保障統計學

生活質量統計學

人口統計學

環境與生態統計學

自然資源統計學

環境統計學

生態平衡統計學

國際統計學

國際標準分類統計學

國際核算體系與方法論體系

國際比較統計學

其他學科

生物統計學

商務統計學

工程統計學

心理統計學

化學統計學

檔案統計學

社會經濟統計學

水文統計學

統計考古學

數理統計學

統計語言學

統計物理學

化學統計學

體育統計學

延伸學科

有些科學廣泛的套用統計的方法使得他們擁有各自的統計術語，這些學科包括：

農業科學

生物統計

商用統計

資料採礦（套用統計學以及圖形從資料中獲取知識）

經濟統計學

電機統計

統計物理學

人口統計

心理統計學

教育統計學

社會統計（包括所有的社會科學）

文獻統計分析

化學與程式分析（所有有關化學的資料分析與化工科學）

運動統計學（特別是棒球以及曲棍球）

統計對於商業以及工業是關鍵的一環，它一般被用來了解與測量系統變異性，程式控制，對資料作出結論，並且完成資料取向的決策，在這些領域統計扮演了一個重要的角色。