基本介紹
- 中文名:中位數
- 外文名:Median
- 別稱:中值
- 歸屬學科:數學
- 基本釋義:一組有序數據中居於中間位置的數
- 領域:統計學;數據挖掘
定義

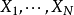



特點
計算示例
例1

例2
Matlab函式



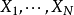





中位數(又稱中值,英語:Median),統計學中的專有名詞,代表一個樣本、種群或機率分布中的一個數值,其可將數值集合劃分為相等的上下兩部分。對於有限的數集,可以...
收入中位數,是指用統計學上中位數的概念來衡量某地區普通民眾的收入水平,相比較於人均收入,收入中位數更貼近普通民眾的實際生活水平,因為某地區的人均收入因貧富...
樣本中位數,是一個數。...... 樣本中位數編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!樣本中位數,是一個數。...
時間中位數是時間中位數即}o百分位數在時間數據中它比平均值更為重要,也更為合理,它較少受極端值的影響。...
房地產市場價格易受極端值(即最高、最低價)影響,而中位數價格能反映市場變動的集中趨勢,代表性比較強。...
分位數(Quantile),亦稱分位點,是指將一個隨機變數的機率分布範圍分為幾個等份的數值點,常用的有中位數(即二分位數)、四分位數、百分位數等。...
樣本頻率分布的中位數。 ...... 樣本頻率分布的中位數。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月第1版,第123頁 V百科往期回顧 詞...
經濟收入中位數是有收入人口(或家庭)經濟收入序列的中間值。西方經濟學中用以反映有收入人口或其家庭收入水平高低的一個指標。經濟收入中位數值上升,說明收入水平...
中位數-極差控制圖是中位數和極差聯合使用的一種控制圖。由於中位數和平均值一樣,反映了數據分布的集中趨勢,所以中位數極差控制圖和平均數-極差控制圖作用基本...
"壽命中位數,活到X歲的一批人再減少一半所要經過的年數,亦稱中位壽命。出生預期壽命中位數(即X=0時)有特殊重要意義。它表明同時期出生的一批人活到剩下一半...
因此,圖基在探索性數據分析中提出了中位數平滑法。這種平滑可以防d:極端值的影響,其平滑方法與移動產均類似,只是在於滑過程中以巾位數代替平均數。這種中位數也稱...
中位數點差是排序後位於數列中間位置的點差值,不受其他點差的極大或極小值影響,能更真實的反映一組點差的真實情況。...
預期壽命中位數是已經活到x歲的一批人減少一半所要經過的年數。對任何一個年齡都可計算預期壽命中位數。如:生命表中50歲的尚存人數150=90000人,76歲的尚存...
低位數:一組數到中後5%的平均數。...... 1 低位數、中位數、高位數的區別 2 舉例說明 低位數低位數、中位數、高位數的區別 編輯 低位數: 一組數到中後5%...
中位數是第50百分位數。第25百分位數又稱第一個四分位數(First Quartile),用Q1表示;第50百分位數又稱第二個四分位數(Second Quartile),用Q2表示;第75百分...
四分位數(Quartile)也稱四分位點,是指在統計學中把所有數值由小到大排列並分成四等份,處於三個分割點位置的數值。多套用於統計學中的箱線圖繪製。它是一組...
常用的主觀機率法有主觀機率加權平均法和累計機率中位數法。 累計機率中位數法是根據累計機率,確定不同預測意見的中位數,對預測值進行點估計和區間估計的預測方法...
《平均模式中位數計算器》是一款Android平台的套用。...... 平均模式中位數計算器套用介紹 編輯 嗨,大家好, 輸入任何數據集,這將計算平均值,模式,中位數和範圍...
中值(又稱中位數)是指將統計總體當中的各個變數值按大小順序排列起來,形成一個數列,處於變數數列中間位置的變數值就稱為中位數。...
它分為正偏態和負偏態。偏態分布的資料有時取對數後可以轉化為常態分配,反映偏態分布的集中趨勢往往用中位數。偏態分布種類 編輯 偏態分布分為正偏態分布和...
