光的衍射
光波遇到障礙物以後會或多或少地偏離幾何光學中直線傳播定律的現象。
幾何光學表明,光在均勻
媒質中按直線定律傳播,光在兩種媒質的分界面按
反射定律和
折射定律傳播。但是,光是一種
電磁波,當一束光通過有孔的屏障以後,其強度可以波及到按直線傳播定律所劃定的幾何陰影區內,也使得幾何照明區內出現某些暗斑或暗紋。總之,
衍射效應使得障礙物後空間的光強分布既區別於幾何光學給出的光強分布,又區別於光波自由傳播時的光強分布,衍射光強有了一種重新分布。衍射使得一切幾何影界失去了明銳的邊緣。義大利物理學家和天文學家F.M.格里馬爾迪在17世紀首先精確地描述了光的衍射現象,150年以後,法國物理學家A.-J.菲涅耳於19世紀最早闡明了這一現象。
介紹
光波遇到障礙物以後會或多或少地偏離幾何光學傳播定律的現象。
 光的衍射
光的衍射光在傳播過程中,遇到障礙物或小孔(窄縫)時,它有離開直線路徑繞到障礙物陰影里去的現象。這種現象叫光的衍射。
衍射時產生的明暗條紋或光環,叫衍射圖樣。
產生條件
產生衍射的條件是:由於光的波長很短,只有十分之幾微米,通常物體都比它大得多,所以當光射向一個針孔、一條狹縫、一根細絲時,可以清楚地看到光的衍射。用單色光照射時效果好一些,如果用複色光,則看到的衍射圖案是彩色的。
光的特點
光的衍射現象的觀察和特點。衍射是一切波所共有的傳播行為。日常生活中聲波的衍射、水波的衍射、廣播段無線電波的衍射是隨時隨地發生的,易為人覺察。但是,光的衍射現象卻不易為人們所覺察,這是因為可見光的波長很短,以及普通光源是非相干的面光源。當用一束強光照明小孔、圓屏、狹縫、細絲、刀口、直邊等障礙物時,在足夠遠的螢幕上會出現一幅幅不同的衍射圖樣。在實驗室中,過去用碳弧燈這類強點光源,而廣泛採用氦氖雷射器作光源來顯示衍射現象,收到了良好的效果(圖1)。衍射現象具有兩個鮮明的特點:
①
光束在衍射屏上的某一方位受到限制,則遠處螢幕上的衍射強度就沿該方向擴展開來。
②若光孔線度越小,光束受限制得越厲害,則衍射範圍越加瀰漫。理論上表明光孔橫向線度ρ與衍射發散角
Δθ之間存在反比關係
ρΔθ≈λ。
當光孔線度遠遠大於光波長
λ時,
衍射效應很不明顯,近似於直線傳播。當光孔線度逐漸變小,衍射效應逐漸明 顯,在遠處便出現亮暗分布的衍射圖樣。當光孔線度小到可以同光波長相比擬時,
衍射效應極為明顯,衍射範圍瀰漫整個視場,過渡為散射情形。
 光的衍射課件
光的衍射課件惠更斯-菲涅耳原理 是處理光的衍射的近似理論,惠更斯-菲涅耳原理可以表述為:
波陣面∑上的每個面元d
∑,可看成為一個新的振源(次波源),它們發出次波;波場中任意處P點的擾動是所有次波到達該點的次級擾動的相干疊加(圖2)。
如用
復振幅(包括振幅和位相)描述波場,若一個次波到達場點的次級擾動為d堚(P), 則場點的總擾動為
式中次級擾動的振幅和位相由以下諸因素決定:
──次波源的微分面積,──次波源本身的復振幅,
 觀察儀器
觀察儀器──傾斜因子,說明次波面源的發射具有一定的方向性。
光的具體形式
60餘年後,G.R.基爾霍夫從定態波場的
亥姆霍茲方程出發,利用矢量場論中的
格林公式,在
kr1近似條件下,導出了無源空間邊值定解的積分形式為式中各量的意義參見圖3,並指明凡是隔離實際點光源與場點的任意閉合面
∑都可以作為積分面(波陣面),它不一定是等相面。上式稱為菲涅耳-基爾霍夫衍射
積分公式,它與由樸素的物理思想所構造的衍射積分相比較,兩者的主體部分是相同的,只是前者明確地給出了傾斜因子和
比例係數的具體形式。
 光的衍射
光的衍射顯然,惠更斯-菲涅耳原理的提出不是為了解決光的自由傳播問題,而是為了求解光通過衍射屏以後的衍射場。為此,取波陣面為包括光孔面
∑o、光屏面
∑1和無窮遠處的半球面
∑2等三部分構成的閉合面。基爾霍夫進一步提出(圖4):
∑0面上的光場堚0(
Q)取自由波場,
∑1面上的光場取0,無窮遠面上的光場對場點的貢獻為0,這稱為基爾霍夫
邊界條件的假設。於是菲涅耳-基爾霍夫衍射公式中的積分區域就限於光孔面。基爾霍夫邊界條件的假設看來是比較自然的,但它並不嚴格成立。光是電磁波,嚴格的衍射理論應是高頻電磁場的矢量波理論。光屏是實物組成的,應考慮光與屏物質(導體或電介質)的相互作用,結果就擾動了光孔面上的原有光場,而且也不會使得光屏面上的光場斷然為0。但是理論表明,嚴格的邊界條件與基爾霍夫邊界條件給出的場分布的顯著差異,僅局限於光屏或光孔邊緣鄰近區域波長量級的範圍內。對於光波,由於其波長往往比光孔的
線度小很多,故採用基爾霍夫邊界條件所產生的誤差不大。但是,對於無線電波的衍射就需要用較嚴格的電磁理論。於是,菲涅耳-基爾霍夫衍射積分式中的積分面只遍及光場不等於零的光孔面
∑0。在光孔和接收範圍滿足旁軸條件下,傾斜因子,衍射積分簡化為式中
r0是
衍射屏中心到場點的距離,上式是計算衍射場的一個實用公式。
 光的衍射觀察儀器
光的衍射觀察儀器衍射系統和衍射屏函式
從衍射積分(傍軸)式中可以看出,對各種衍射屏來說積分核是相同的,衍射場的不同分布是由瞳函式堚0(
Q)或光場不等於零的光孔面
∑0的形狀和大小等兩方面的差別而引起的。可能導致光波衍射的障礙物(屏)的品種是多種多樣的,凡是使波陣面上的復振幅分布發生改變的物,統稱為衍射屏。衍射屏可以是反射物或透射物,諸如圓孔、矩孔、單縫等一類中間開孔型的,有小球、細絲、墨點、顆粒等一類中間阻擋型的,有反射閃耀光柵、透射黑白光柵、菲涅耳波帶片、
正弦型光柵等周期型的,也可以是景物的一幅底片、一張圖像、一頁數碼字元等複雜型的,還可能是透鏡稜鏡等一類位相型的衍射屏。
 光的衍射
光的衍射以衍射屏為界,整個衍射系統分成前後兩部分(圖5)。前場為照明空間,充滿照明光波;後場為衍射空間,充滿衍射光波。照明光波的波型一般比較簡單,常用
球面波或
平面波,這兩種典型波的等相面與等幅面是重合的,屬於均勻波,其波場中沒有因光強起伏而出現的亮暗圖樣。衍射波比較複雜,它不是單純的一束球面波或平面波,其等相面與等幅面一般不重合,屬於非均勻波,其波場中常有光強起伏形成的衍射圖樣。在衍射系統分析中注重三個場分布。一是衍射屏左側的入射場堚1(
x,
y),它是入射光波陣面函式;二是衍射屏右側的透射場堚2(
x,
y),當然也可以是反射場,它是衍射場波陣面函式;三是衍射波向前傳播而到達接收螢幕上的光場函式 堚(
x′,
y′)。將堚1場變換為堚2場的是衍射屏的作用,由堚2場導出堚場是衍射問題的基本提法,也是
光的傳播問題的基本提法,其理論根據就是惠更斯-菲涅耳原理。由此可見,本質上說,光波衍射就是波陣面變換。
 光的衍射
光的衍射衍射種類
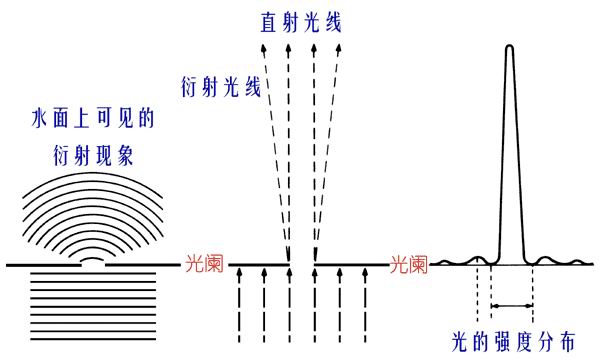
狹縫衍射
讓雷射發出的單色光照射到狹縫上,當狹縫由很寬逐漸減小,在光屏上出現的現象怎樣?
當狹縫很寬時,縫的寬度遠遠大於光的波長,衍射現象極不明顯,光沿直線傳播,在屏上產生一條跟縫寬度相當的亮線;但當縫的寬度調到很窄,可以跟光波相比擬時,光通過縫後就明顯偏離了直線傳播方向,照射到屏上相當寬的地方,並且出現了明暗相間的衍射條紋,紋縫越小,衍射範圍越大,衍射條紋越寬。但亮度越來越暗。
 光的衍射圖樣1
光的衍射圖樣1試驗:可以用遊標卡尺調整到肉眼可辨認的最小距離,再通過此縫看光源。
 光的衍射圖樣2
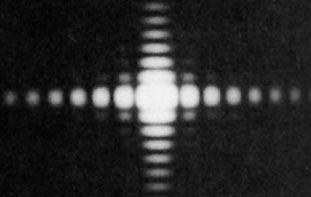
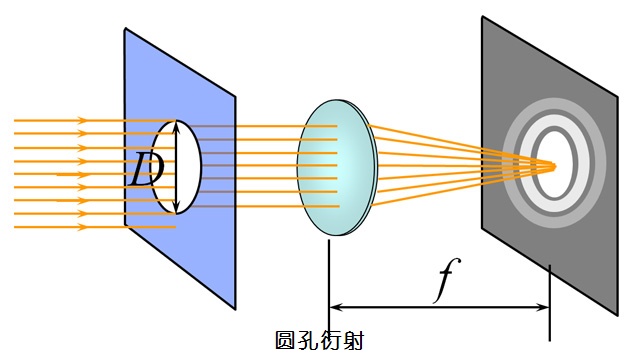
光的衍射圖樣2小孔衍射
當孔半徑較大時,光沿直線傳播,在屏上得到一個按直線傳播計算出來一樣大小的亮光圓斑;減小孔的半徑,屏上將出現按直線傳播計算出來的倒立的光源的像,即
小孔成像;繼續減小孔的半徑,屏上將出現明暗相間的圓形衍射光環。
 光的衍射
光的衍射衍射套用
光的衍射決定光學儀器的分辨本領。氣體或液體中的大量懸浮粒子對光的散射,衍射也起重要的作用。在現代光學乃至
現代物理學和科學技術中,光的衍射得到了越來越廣泛的套用。衍射套用大致可以概括為以下五個方面:
 光的衍射
光的衍射① 衍射用於光譜分析。如衍射光柵光譜儀。
② 衍射用於結構分析。衍射圖樣對精細結構有一種相當敏感的“放大”作用,故而利用圖樣分析結構,如X射線結構學。
⑤.X光的衍射可用於測定晶體的結構,這是確定晶體結構的重要方法。
相關介紹
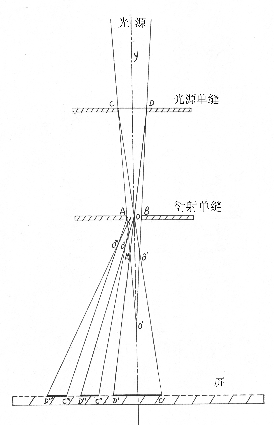
實驗室里觀察衍射現象
實驗室里為了觀察
衍射現象,總是由光源、衍射屏和接收衍射圖樣的螢幕(稱為接收屏)組成一個衍射系統。為了研究的方便,通常根據衍射系統中三者的相互距離的大小,將衍射現象分為兩類,一類稱為菲涅耳衍射,另一類稱為
夫琅禾費(J.Fraunhofer,1787- 1826)衍射。所謂菲涅耳衍射,就是當光源到衍射屏的距離或接收屏到衍射屏的距離不是無限大時,或兩者都不是無限大時所發生的衍射現象。可見在菲涅耳衍射中,
入射光或衍射光不是平行光,或兩者都不是平行光,如圖13-15(a)所示。所謂
夫琅禾費衍射,就是當光源到衍射屏的距離和接收屏到衍射屏的距離都是無限大時,所發生的衍射現象。可見在夫琅禾費衍射中入射光和衍射到接收屏上任意一點的光都是平行光,如圖13-15(b)所示。夫琅禾費衍射的條件在實驗室里可藉助於
透鏡實現。將光源放置在會聚透鏡L1的焦點上,則從L1透射的光,即衍射孔的入射光就是平行光;同時將接收屏放置在會聚透鏡L2的焦面上,則到達接收屏上任意一點的衍射光也是平行光。
 光的衍射
光的衍射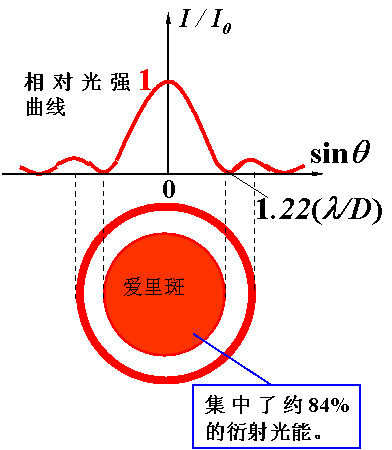 夫琅禾費衍射
夫琅禾費衍射 光的衍射
光的衍射 光的衍射課件
光的衍射課件 觀察儀器
觀察儀器 光的衍射
光的衍射 光的衍射觀察儀器
光的衍射觀察儀器 光的衍射
光的衍射 光的衍射
光的衍射 光的衍射圖樣1
光的衍射圖樣1 光的衍射圖樣2
光的衍射圖樣2 光的衍射
光的衍射 光的衍射
光的衍射 光的衍射
光的衍射 夫琅禾費衍射
夫琅禾費衍射
