簡介
波動光學是光學中非常重要的組成部分,內容包括
光的干涉、光的
衍射、光的
偏振等,無論理論還是套用都在物理學中占有重要地位。
粒子在光場或其他
交變電場的作用下,形成振盪的
偶極子,發出
次波。利用這種觀點來說明光的
色散、
吸收、散射、磁光效應、
電光效應等現象,甚至光的
發射也是一般波動光學的內容。
電磁波理論套用到晶體稱
晶體光學。
光波在真空中的波長約為(3.9~7.6)×10
-5cm,一般的
障礙物或孔隙都遠大於此,因而通常都顯示出
光的直線傳播現象。這一時期,人們還發現了一些與光的
波動性有關的光學現象,例如F.M.
格里馬爾迪首先發現光遇障礙物時將偏離直線傳播,他把此現象起名為“
衍射”。胡克和R.
玻意耳分別觀察到現稱之為
牛頓環的
干涉現象。這些發現成為波動光學發展史的起點。17世紀以後的一百多年間,
光的微粒說(見
光的二象性)一直占統治地位,
波動說則不為多數人所接受,直到進入19世紀後,光的波動理論才得到迅速發展。
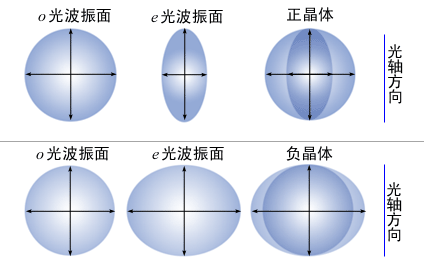 晶體光學
晶體光學詳細介紹
18世紀
1800年,T. 楊提出了反對微粒說的幾條論據,首次提出干涉這一術語,並分析了水波和
聲波疊加後產生的
干涉現象。楊於1801年最先用雙縫演示了
光的干涉現象(見楊氏實驗),第一次提出波長概念,並成功地測量了
光波波長。他還用干涉原理解釋了白光照射下薄膜呈現的顏色。1809年E. L.
馬呂斯發現了反射時的
偏振現象(見
布儒斯特定律),隨後A.-J.
菲涅耳和D. F. J.
阿拉戈利用楊氏實驗裝置完成了
線偏振光的疊加實驗,楊和菲涅耳藉助於光為
橫波的假設成功地解釋了這個實驗。1815年,菲涅耳建立了
惠更斯-菲涅耳原理,他用此原理計算了各種類型的孔和直邊的
衍射圖樣,令人信服地解釋了衍射現象。1818年關於阿拉戈斑(見菲涅耳衍射)的爭論更加強了
菲涅耳衍射理論的地位。至此,用光的波動理論解釋
光的干涉、衍射和偏振等現象時均獲得了巨大成功,從而牢固地確立了
波動理論的地位。
19世紀
19世紀60年代,J. C.
麥克斯韋建立了統一
電磁場理論,預言了電磁波的存在並給出了電磁波的
波速公式。隨後H. R.
赫茲用實驗方法產生了電磁波。光與
電磁現象的一致性使人們確信光是電磁波的一種,光的經典波動理論與
電磁理論融成了一體,產生了光的電磁理論。將電磁理論套用於晶體,對光在晶體中的傳播規律給出了嚴格而圓滿的解釋。19世紀末,H. A.
洛倫茲創立了
電子論,他把物質的巨觀性質歸結為構成物質的電子的
集體行為。電磁波的作用使帶電
粒子產生
受迫振動並產生次級電磁波,根據這一理論解釋了
光的吸收、
色散和散射等分子光學現象。這種經典的電磁理論並非十全十美,因在關於光與物質相互作用的問題上涉及微觀粒子的行為,必須用
量子理論才能得到徹底的解決。
波動光學的研究成果使人們對光的本性的認識得到了深化。在套用領域,以干涉原理為基礎的干涉計量術為人們提供了
精密測量和檢驗的手段(見
干涉儀),其精度提高到前所未有的程度;
衍射理論指出了提高光學儀器
分辨本領的途徑(見夫琅和費衍射);
衍射光柵已成為分離
光譜線以進行
光譜分析的重要
色散元件;各種
偏振器件和儀器用來對岩礦晶體進行檢驗和測量,等等。所有這些構成了套用光學的主要內容。
 偏振片
偏振片20世紀
發展史
十七世紀
從十七世紀開始,就發現有與
光的直線傳播不完全符合的事實。義大利人格里馬第(1618~1663)首先觀察到
光的衍射現象,他發現在
點光源的照射下,一根直竿形成的影子要比假定光以直線傳播所應有的寬度稍大一些,也就是說光並不嚴格按直線傳播,而會繞過
障礙物前進。接著,1672 ~1675年間胡克(1635~1703)也觀察到
衍射現象,並且和
玻意耳(1627~1691)獨立的研究了薄膜所產生的彩色干涉條紋,所有這些都是光的波動理論的萌芽。 十七世紀下半葉,
牛頓(1642~1727)和
惠更斯(1629~1695)等把光的研究引向進一步發展的道路。牛頓的白光實驗以及牛頓圈的發現,使光學由
幾何光學進入了波動光學。惠更斯最早比較明確的提出了
光的波動說。在《論光》(1690)一書中,他認為光的運動不是物質微粒的運動而是
媒質的運動即波動,運用
波動說,他很好的解釋了
光的反射,折射以及
方解石的
雙折射現象。
 牛頓
牛頓十九世紀
19世紀的光學是由英國醫生
托馬斯·楊以復興
波動說的論文揭開序幕的。1801年,楊向皇家學會宣讀了關於薄片顏色的論文,文中正式將干涉原理引入到光學之中,並且用這一原理解釋薄片上的顏色和條紋面的
衍射。在這篇論文中,楊還系統提出了波動光學的基本原理,提出了
光波長的概念,並給出了測定結果。正是由於光波長太短,以至遇
障礙物拐彎能力不大,這也是人們很難觀察到這類現象的原因。又於1803年發表了物理光學的實驗和計算,對
雙縫干涉現象進一步作出了解釋。在1807年出版的《自然哲學講義》中,楊系統闡述了他提出的波動光學的基本原理。
幾乎獨立的提出的波動說的還有法國物理學家菲涅爾(1788~1827)。1815年,他向科學院提交了第一篇光學論文,文中仔細研究了
光的衍射現象,並提出了
光的干涉原理。後來,菲涅爾與楊齊心協力,在波動學說基礎上的光學實驗大量湧現,使19世紀在波動光學方面取得了重大發展。
折射現象
光的折射
光的衍射是光的
波動性的重要標誌之一,光在傳播過程中所呈現的
衍射現象,進一步揭示了光的波動本性。同時
衍射也是討論現代光學問題的基礎。 波在傳播中表現出衍射現象,既不沿直線傳播而向各方向
繞射的現象。窗戶內外的人,雖然彼此不相見,都能聽到對方的說話聲,這說明
聲波(
機械波的一種)能饒過窗戶邊緣傳播。水波也能繞過水麵上的
障礙物傳播。無線電波能繞過山的障礙,使山區也能接受到電台的廣播。這些現象表明,當波遇到障礙物時,它將偏離直線傳播,這種現象叫做
波的衍射。
光由一種介質進入到另一介質而偏離直線傳播的現象,叫做
光的折射。
光的傳播
光的傳播看來是沿直線進行的,遇到不透明的
障礙物時,會投射出清晰的影子,粗看起來,
衍射和直線傳播似乎是彼此矛盾的現象。
光的干涉
光的干涉現象是幾束光相互疊加的結果。實際上即使是單獨的一束光投射在屏上,經過精密的觀察,也有明暗條紋花樣出現。例如把楊氏干涉實驗裝置中光闌上兩個小孔之一遮蔽,使
點光源發出的光通過單孔照射到屏上,仔細觀察時,可看到屏上的明亮區域比根據
光的直線傳播所估計的要大得多,而且還出現明暗不
均勻分布的照度。光通過狹縫,甚至經過任何物體的邊緣,在不同程度上都有類似的情況。把一條金屬細線(作為對光的
障礙物)放在屏的前面,在影的中央應該是最暗的地方,實際觀察到的卻是亮的,這種光線繞過障礙物偏離直線傳播而進入幾何陰影,並在螢幕上出現光強不均勻的分布的現象叫做
光的衍射。
 複色光的衍射
複色光的衍射 光的衍射現象的發現,與
光的直線傳播現象表現上是矛盾的,如果不能以波動觀點對這兩點作統一的解釋,就難以確立光的
波動性概念。事實上,
機械波也有直線傳播的現象。超
聲波就具有明顯的方向性。普通聲波遇到巨大的障礙物時,也會投射清楚的影子,例如在高大牆壁後面就聽不到前面的的聲響。在海港
防波堤裡面,巨大的海浪也不能到達。微波一般也同樣是以直線傳播的。
衍射現象的出現與否,主要決定於
障礙物線度和波長大小的對比。只有在障礙物線度和波長可以比擬時,衍射現象才明顯的表現出來。聲波的波長可達幾十米,無線電波的波長可達幾百米,它們遇到的障礙物通常總遠小于波長,因而在傳播途中可以繞過這些障礙物,到達不同的角度。一旦遇到巨大的障礙物時,直線傳播才比較明顯。超
聲波的波長
數量級小的只有幾毫米,微波波長的數量級也與此類似,通常遇到的障礙物都遠較此為大,因而它們一般都可以看作是直線傳播。
光波波長
光波在真空中的波長約為(3.9~7.6)×10
-5cm ,一般的
障礙物或孔隙都遠大於此,因而通常都顯示出光的直線傳播現象。一旦遇到與波長差不多
數量級的障礙物或孔隙時,
衍射現象就變的顯著起來了。
衍射現象
光的
衍射是光的波動性的重要標誌之一,光在傳播過程中所呈現的衍射現象,進一步揭示了光的波動本性。同時衍射也是討論現代光學問題的基礎。
波在傳播中表現出衍射現象,既不沿直線傳播而向各方向繞射的現象。窗戶內外的人,雖然彼此不相見,都能聽到對方的說話聲,這說明
聲波(機械波)能饒過窗戶邊緣傳播。水波也能繞過水麵上的障礙物傳播。無線電波能繞過山的障礙,使山區也能接受到電台的廣播。這些現象表明,當波遇到障礙物時,它將偏離直線傳播,這種現象叫做波的衍射。
光的傳播看來是沿直線進行的,遇到不透明的障礙物時,會投射出清晰的影子,粗看起來,衍射和直線傳播似乎是彼此矛盾的現象。
光的
干涉現象是幾束光相互疊加的結果。實際上即使是單獨的一束光投射在屏上,經過精密的觀察,也有明暗條紋花樣出現。例如把楊氏干涉實驗裝置中光闌上兩個小孔之一遮蔽,使點
光源發出的光通過單孔照射到屏上,仔細觀察時,可看到屏上的明亮區域比根據光的直線傳播所估計的要大得多,而且還出現明暗不均勻分布的照度。光通過狹縫,甚至經過任何物體的邊緣,在不同程度上都有類似的情況。把一條
金屬細線(作為對光的障礙物)放在屏的前面,在影的中央應該是最暗的地方,實際觀察到的卻是亮的,這種光線繞過障礙物偏離直線傳播而進入幾何陰影,並在螢幕上出現光強不均勻的分布的現象叫做光的衍射。
光的衍射現象的發現,與光的直線傳播現象表現上是矛盾的,如果不能以波動觀點對這兩點作統一的解釋,就難以確立光的波動性概念。事實上,
機械波也有直線傳播的現象。
超音波就具有明顯的方向性。普通聲波遇到巨大的障礙物時,也會投射清楚的影子,例如在高大
牆壁後面就聽不到前面的的聲響。在海港防波堤裡面,巨大的海浪也不能到達。
微波一般也同樣是以直線傳播的。
衍射現象的出現與否,主要決定於障礙物線度和波長大小的對比。只有在障礙物線度和
波長可以比擬時,衍射現象才明顯的表現出來。聲波的波長可達幾十米,無線電波的波長可達幾百米,它們遇到的障礙物通常總遠小于波長,因而在
傳播途中可以繞過這些障礙物,到達不同的角度。一旦遇到巨大的障礙物時,直線傳播才比較明顯。超音波的波長數量級小的只有幾毫米,微波波長的數量級也與此類似,通常遇到的障礙物都遠較此為大,因而它們一般都可以看作是直線傳播。
與幾何光學關係
與
可見光傳播相關聯的
電磁場,其特點是振動非常之快(頻率
數量級為10s),或者說是波長非常短(數量級為10
-15cm)。因此可以預期,在這種情況下,完全忽略波長的有限大小,可以得到光傳播定律的良好一級近似。人們發現,對很多光學問題而言,這樣處理是完全適合的。在光學中,可以忽略波長,即相當於
λ0→0 極限情況的這一分支,通常稱為
幾何光學,因為在這種近似處理下,光學定律可以用幾何學的語言來表述。
衍射現象的一個最簡單的典型例子——單
狹縫的夫琅和費衍射。它包含著衍射現象的許多主要特徵。來自光源
S的光(例如雷射)經望遠鏡系統構成的擴束器
L1擴束直接投射到一狹縫上。在狹縫後面放置一
透鏡L2,那么在透鏡
L2的
焦平面上放置的螢幕
F'
F上將產生明暗交替的
衍射花樣。其特點是在中央具有一特別明亮的亮條紋,兩側排列著一些強度較小的亮條紋。相鄰的亮條紋之間有一暗條紋。如以相鄰暗條紋之間的間隔作為亮條紋的寬度,則兩側亮條紋為等寬的,而中央亮條紋的寬度為其它條紋的兩倍。人們將亮條紋到透鏡中心所張的角度稱為角寬度。中央亮條紋和其它亮條紋的角寬度不相等。中央亮條紋的角度等於 2
λ/
b(
b為縫寬),即等於其它亮條紋角寬度的2倍。那么中央亮紋的半角寬度 Δ
θ=
λ/
b,正好等於其它亮紋的角寬度。
 光的折射
光的折射由於中央亮斑集中了大部分光能,所以它的半角寬度 的大小可作為
衍射效應強弱的量度。式子Δ
θ=
λ/
b告訴我們,對給定的波長,Δ
θ與縫寬
b成反比,即在
波前上對
光束限制越大,
衍射場越彌散,衍射斑鋪開的越寬;反之當縫寬很大,光束幾乎自由傳播時,Δ
θ→0,這表明衍射場基本上集中在沿直線傳播的方向上,在
透鏡焦平面上衍射斑收縮為
幾何光學象點。式子Δ
θ=
λ/
b還告訴我們,在保持縫寬不變的條件下,Δ
θ與
λ成正比,波長越長,
衍射效應越顯著;波長越短,衍射效應越可忽略。所以說幾何光學是
b>>
λ時的一種近似,或說
λ→0的近似。除了直線傳播定律之外,作為幾何光學基礎的另外兩條定律-
反射定律和
折射定律,也都只在入很小的條件下才近似成立,所以幾何光學原理的適用範圍是有限度的,在必要的時候需要用更嚴格的波動理論來代替它。不過由於
幾何光學處理問題的方法要簡單的多,並且它對各種光學儀器中遇到的許多實際問題已足夠精確,所以幾何光學並不失為各種光學儀器的重要理論基礎。
相關學科
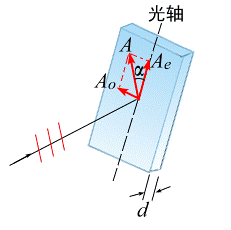
 晶體光學
晶體光學 牛頓
牛頓 光的折射
光的折射
 晶體光學
晶體光學 牛頓
牛頓 光的折射
光的折射