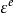簡介,基本實驗和基本理論,基本實驗,基本假設,簡化模型,屈服條件和本構關係,研究內容,塑性力學的平面問題,塑性極限分析,塑性動力學,粘塑性理論,結構的塑性穩定性問題,求解方法,靜定法,滑移線法,界限法,參數方程法,加權殘量法,有限元法,主要套用,發展簡史,
簡介
固體力學的一個分支,研究物體超過彈性極限後所產生的永久變形和作用力之間的關係以及物體內部應力和應變的分布規律。和彈性力學的區別在於,塑性力學考慮物體內產生的永久變形,而彈性力學不考慮,和流變學的區別在於,塑性力學考慮的永久變形只與應力和應變的歷史有關而不隨時間變化,而流變學考慮的永久變形與時間有關。
一般將塑性力學分為數學塑性力學和套用塑性力學,其含義同將彈性力學的分為數學彈性理論和套用彈性力學是類似的。前者是經典的精確理論,後者是在前者各種假設的基礎上,根據實際套用的需要,再加上一些補充的簡化假設而形成的套用性很強的理論。從
數學上看,套用塑性力學粗糙一些,但從套用的角度看,它的方程和計算公式比較簡單,並且能滿足很多結構設計的要求。
塑性力學理論在工程實際中有廣泛的套用。例如用於研究如何發揮材料強度的潛力,如何利用材料的塑性性質,以便合理選材,制定加工成型工藝。塑性力學理論還用於計算殘餘應力。
基本實驗和基本理論
基本實驗
從學科建立過程來看,塑性力學是以實驗為基礎,從實驗中找出受力物體超出
彈性極限後的變形規律,據以提出合理的假設和簡化模型,確定應力超過彈性極限後材料的本構關係,從而建立塑性力學的基本方程。解出這些方程,便可得到不同塑性狀態下物體中的應力和
應變。
塑性力學的基本實驗主要分兩類:單向拉伸實驗和
靜水壓力實驗。通過單向拉伸實驗可以獲得載入和卸載時的
應力-應變曲線以及彈性極限和
屈服極限的值;在塑性狀態下,應力和應變之間的關係是非線性的且沒有
單值對應關係。由
靜水壓力實驗得出,靜水壓力只能引起金屬材料的彈性變形且對材料的
屈服極限影響很小(岩土材料則不同)。
1單拉伸實驗
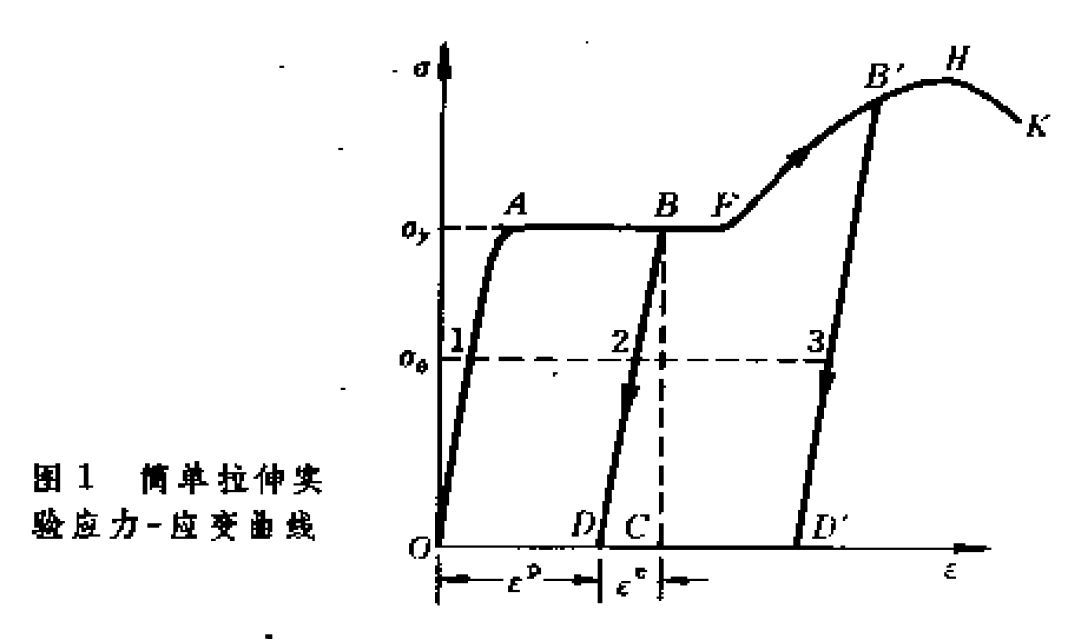
對某些材料(如低碳鋼)作簡單拉伸實驗,可得到如圖1所示的應力-應變曲線。實驗表明,應力-應變曲線上存在一個稱為彈性極限的應力值,若應力小於彈性極限,則載入和卸載的應力-應變曲線相同(
OA段);若應力超過彈性極限,載入的應力-應變曲線有明顯的轉折,並出現一個水平的線段(AF),常稱為屈服階段,相應的應力稱為屈服極限。彈性極限、屈服極限的值相差不大,在工程上常取為一個值,仍稱屈服極限,記為
材料中的應力達到屈服極限時,材料即進入塑性階段。此階段的最大特點是:載入和卸載的應力-應變曲線不同。例如由圖1中B點卸載,應力與應變不是沿BAO線而是沿著BD線退回。應力全部消失後,仍保留永久應變OD。實驗表明,在變形不大時,多數材料應力-應變曲線中的BD與OA接近平行,以
表示塑性應變OD,表示彈性應變DC,則B點的應變為:
如果從D點重新載入,開始時仍沿DB變化,在回到B點後則按BFH變化並產生新的塑性變形。若在卸載至,則再載入時,點的應力成為新的屈服極限,它高於初始屈服極限
這一現象成為應變強化或加工強化。點的應力稱為後繼屈服極限或載入應力。對於均勻應力狀態,外載全部卸除後,巨觀應力等於零,但保留了巨觀的殘餘應變。實際上,物體內部微觀結構發生了變化,產生了微觀的殘餘應力,它能在下次載入時擴大物體的彈性範圍。J.包辛格於1886年發現,在卸載後施加反方向壓力時,反向屈服極限降低了。這一現象後為
包辛格效應,它是上述微觀殘餘應力造成的。
由簡單應力狀態的應力-應變曲線可以看出,塑性力學問題有兩個主要特點:一是應力與應變之間的關係是非線性的;二是應力與應變之間的關係不是單值對應的,而與載入歷史有關。例如圖1中,同一應力視載入歷史的不同可對應1、2、3點的應變。因此塑性力學的問題是從某一已知初始狀態開始,隨著載入過程,用應力增量與應變增量的關係逐步求出每時刻的增量,累加起來得到物體內的最終應力和應變分布。
②靜水壓力實驗
實驗表明,靜水壓力可使材料的可塑性增加,原來處於脆性狀態的材料可以轉化成為塑性材料。但靜水壓力對金屬材料的屈服極限影響不大(岩石材料則不同)。平均正應力在幾萬個大氣壓以內時,金屬材料的體積變化與平均正應力近似成正比。
基本假設
為簡化計算,根據實驗結果,塑性力學採用的基本假設有:①材料是各向同性和連續的。②平均
法向應力不影響材料的屈服,它只與材料的體積應變有關,且體積應變是彈性的,即靜水壓力狀態不影響
塑性變形而只產生彈性的體積變化。這個假定主要根據是著名的Brid-gman試驗。③材料的彈性性質不受塑性變形的影響。這些假設一般適用於金屬材料;對於岩土材料則應考慮平均
法向應力對屈服的影響。④只考慮穩定材料,即不考慮塑性應變的弱化階段(圖1中的HK段)。此外,在一般的塑性靜力問題中,還假設時間因素對材料的性質沒有影響。變形速度、應變率、應力率等概念往往只表示位移、應變、應力的增量,這些增量在多長時間內產生,對分析問題沒有影響。以上假設適用於一般金屬材料,對於岩土材料則需考慮平均正應力對屈服的影響及彈塑性耦合問題。
簡化模型
①理想彈塑性模型對低碳鋼或強化性質不明顯的材料,若應變不太大,則可忽略強化因素,而將實際應力-應變曲線(圖2中的虛線)簡化為折線,如圖2所示,圖中0-1線表示理想彈性,1-2表示理想塑性。
②線性強化彈塑性模型對有顯著強化性質的材料,可用兩條直線代替實際曲線(圖3)。
③理想剛塑性模型對彈性應變比塑性應變小得多而且強化性質不明顯的材料,可用水平直線代替實際曲線(圖4)
④線性強化剛塑性模型對彈性應變比塑性應變小得多而且強化性質明顯的材料,可用傾斜直線代替實際曲線(圖5)
⑤冪次強化模型為簡化計算中的解析式,可用冪次強化模型(圖6),其解析表達式為
屈服條件和本構關係
在複雜應力狀態下,各應力分量成不同組合狀態的屈服條件以及應力分量和應變分量之間的塑性本構關係是塑性力學的主要研究內容,也是分析塑性力學問題時依據的物理關係。
屈服條件是判斷材料處於彈性階段還是處於塑性階段的判據。對於金屬材料,最常用的屈服條件為最大
剪應力屈服條件(又稱特雷斯卡屈服條件)和
彈性形變比能屈服條件(又稱米澤斯屈服條件)。這兩個屈服條件數值接近,它們的數學表達式都不受靜水壓力的影響,而且基本符合實驗結果。對於理想塑性模型,在經過塑性變形後,屈服條件不變。但如果材料具有強化性質,則屈服條件將隨塑性變形的發展而改變,改變後的屈服條件稱為後繼屈服條件或載入條件(見強化規律)。對於岩土材料則常用特雷斯卡屈服條件、德魯克-普拉格屈服條件和莫爾-庫倫屈服條件。當已知主應力的大小次序時,使用特雷斯卡屈服條件較為方便;若不知道主應力的大小次序,則使用米澤斯屈服條件較為方便。對於韌性較好的材料,米澤斯屈服條件與試驗數據符合較好。
反映塑性應力-應變關係的本構關係,一般應以增量形式給出,這是因為塑性力學中需要考慮變形的歷程,而增量形式可以反映出變形的歷程,反映塑性變形的本質。用增量形式表示塑性本構關係的理論稱為塑性增量理論。研究表明,應力和應變的增量關係與屈服條件有關。增量理論的本構關係在理論上是合理的,但套用起來比較麻煩,因為需要積分整個變形路徑才能得到最後的結果。因此,在塑性力學中又發展出塑性全量理論,即採用全量形式表示塑性本構關係的理論。在單向應力狀態下,若限定應力只增不減(即只載入不卸載),則應力全量與應變全量之間就有直接關係,如同非線性彈性關係那樣。在複雜應力狀態下,若各應力分量按一定比例增長(稱為比例載入)而不卸載,則可將增量關係積分得全量關係,但一般情形下,各應力分量之間的比例是有變化的,嚴格來說,不能得出全量關係。然而全量關係使用方便,因而常用與求解實際問題。研究表明:在偏離比例載入不大時,全量理論的計算結果和實驗接近,至於允許偏離的程度,尚無定量的標準。
解決塑性力學的邊值問題,所使用的平衡方程、幾何方程(即應變和位移的關係)以及力和位移的邊界條件都和彈性力學中所使用的相同,但在物理關係上則應以全量理論或增量理論的塑性本構關係代替彈性力學中的廣義胡克定律(見胡克定律)。利用平衡方程、幾何方程、物理關係和所有邊界條件可以求得超過屈服極限後的應力和應變分布以及內力和外載荷之間的關係。但是塑性力學的本構關係是非線性的,在具體計算邊值問題時會遇到一些數學上的困難,因此在塑性力學中還要根據所研究問題的具體情況,找出解決方法。
研究內容
除上述基本理論以外,塑性力學還包括以下研究內容:
簡單彈塑性問題經過簡化只剩下一個獨立變量的問題
這類問題有:
梁的彈塑性彎曲問題
如果像處理彈性彎曲問題一樣引用平截面假設,則梁的彈塑性彎曲問題就成為一維問題目。在彎矩M的作用下,梁截面上的正應力分布為其中x為梁縱軸坐標,y為截面上的坐標, y=O對應於中性軸,I為截面繞中性軸的慣性矩。對一個寬為b、髙為h的矩形截面梁,。當最外層纖維的應力達到屈服極限時,作用在截面上的彎矩為彈性極限彎矩。如果彎矩繼續增加,則外層纖維首先進入塑性變形階段,從梁截面上看,塑性變形區隨 彎矩的增加向中心發展,純彈性變形區逐漸縮小。在極限情形,彈性區縮小為零。對於理想塑性材料,與極限情形對應的彎矩稱為塑性極限彎矩,其值為這一結果意味著,如果允許梁內發生塑性變形,矩形截面梁的抗彎矩能力最多可以提髙50%。彎矩達到塑性極限彎矩前梁的變形仍屬彈性量級。因此,在設計中可讓梁內發生部分塑性變形以提高梁的承載能力。一般說來,梁的靜不定次數(見靜不定結構)愈高,承載能力提髙的幅度愈大。
受內壓厚壁圓筒問題
研究對象是一個內半徑為外半徑為,並且受內壓P作用的長厚壁筒。這是—個軸對稱問題,可在以筒軸為z軸的柱坐標系中進行研究。若考慮軸向應力的情形,則壁內的 兩個主應力為和,最大剪應力屈服條件可寫成。根據彈性分析可知在內壁處最大。當壓力時,內壁開始產生塑 性變形。塑性區隨著壓力的增加而向外擴展。在分析這一問題時,要區分彈性和塑性區,在不同區域中使用不同的應力-應變關係;另外還要求各物理參量(應力、應變 等)在彈性區和塑性區的交界面上滿足連線條件和初始屈服條件。由這兩個條件可定出彈塑性交界面的位置。 對於理想塑性材枓,當應力滿足屈服條件時,材料可無限 制地發生塑性變形。但實際上,塑性區的變形受到外層 彈性區的約束,不能無限發展,材料處在約束塑性變形階段。當塑性區擴展到外邊界處時,外層的彈性約束消失,塑性變形可以自由發展,這時所對應的壓力稱為塑性極限壓力,其值為。若在到達塑性極限壓力前卸載,壁內就產生殘餘應力。再次載入時,應力將從 這個殘餘應力上增長。和簡單拉伸時的情形一樣,殘餘 應力可使彈性範圍提髙到卸載前的最高值。利用殘餘應力的這一特性,可以延長大炮筒及其他壓力賽器的使用壽命。
長柱體的塑性自由扭轉問題
按照彈性力學中 解決此類問理的方法引進應力函式(見柱體扭轉和彎曲),把不為零的剪應力表示為:
則平衡方程自動滿足。最大剪應力出現在柱體邊界上,式中▽為梯度算符。當扭矩增大到彈性極限時,邊界上某些點處為剪下屈服極限,塑性變形首先在那些點產生。隨著扭 矩的增大,塑性區向內發展.對於理想塑性材料,在塑性 區內為一常數。另外,從邊界條件的要求可 知,邊界上。塑性區內的函式可用邊界上的等梯度斜面表示。取柱體的一個截面,當整個截面進入塑性 屈服階段時,那些邊界上的斜面匯交成一個在此截面上 的沙堆形狀包絡面,沙堆體積的兩倍對應於塑性極限扭矩。這種用沙堆體積計算柱體極限扭矩的方法就稱為塑性扭轉問題中的沙堆比擬法,通過它可以求得較複雜截 面柱的極限彎矩和剪應力分布規律。
塑性力學的平面問題
這類問題可分為:
塑性平面應變問題
金屬壓力加工中的薄板軋制、拉拔、擠壓等問題即屬於塑性平面應變問題。這種問題的特點是:應變被限制在一個平面內。這種問題的塑 性變形比彈性變形大得多,故可採用剛塑性模型。在 建工程中,邊坡穩定問題和長條形地基基礎問題等也可作為塑性平面應變問題。塑性平面應變問題有三個方程:兩個平衡方程和一個屈服條件方程。如果邊界上給定的是應力條件,則可利用三個方程求出應力的分布,而且不需要使用塑性本構關係。在得到問題的解後,應校核剛性區內各點的應力是否滿足屈服條件,只有不滿足屈服條件,解才算是一個靜力允許解;另外,還要校核所得的解給出的位移速度能否滿足位移速度的邊界條件以及外 力在這個位移速度上是否作正功率的條件,如果又滿足 這些條件,解才是一個完全解。塑性平面應變問題可以用滑移線法求解。對於土力學問題,在平衡方程中,還要考慮重力項。
塑性平面應力問題主要出現在薄板中。
有塑性變形的薄板中孔洞附近的應力集中問題、圓孔的擴張 問題和薄板的彎曲問題等均屬塑性平面權力問題.在塑性平面應力問題中,沿厚度z方向的應力等於零。設在板平面內的主應力為,則屈服條件為。在應力滿足屈服條件時,板中可能產生垂直於板平面的剪下滑動,造成在板平面上看來垂直於滑動方向的速度間斷,並會引起厚度變化等複雜問題。
塑性極限分析
對於理想塑性材料,當外載荷達到某個極限值時,塑性區的變形不再受約束,材料處於塑性流動狀態,即材料奇以無限制地變形,這種狀態稱為塑性極限狀態,與此狀態對應的載荷稱為塑性極限載荷。對物體在塑性極限狀態下特性的研宄稱為塑性極限分析,其主要目的是求出塑性極限栽荷,有兩種方法:一種方法是,同時考慮彈性變形和塑性變形,求出塑性區的擴展和載荷的關係,最後求得塑性極限載荷;另一種方法是,忽略彈性變形而採用剛塑性模型求出塑性極限載荷。這兩種方法所得的結果是相同的。由於第一種方法比較複雜,所以通常採用第二種方法。在用上述兩種方法求解複雜問題時,可根據塑性極限分析的上、下限定理(見結構塑性極限分析),對塑性極限載荷作出足夠精確的估計。除了求塑性極限載荷外,塑性極限分析還可用於尋找結構在塑性極限狀態下的破壞形式,以及用於估計金屬塑性成型中的外力和構件的變形。
塑性動力學
研究各種彈塑性或結構在短時強載荷作用下的應力、變形和運動規律。由於物體有慣性,所以對物體突加強載荷不可能同時擾動物體各部分質點,擾動須經過一個傳播過程才能由擾動區逐步傳播到未擾動區。外力對於物體的動力效應需要通過分析塑性波的傳播來研究,這類問題稱為塑性波的傳播問題。在實際中,一般都使梁、板、殼等結構在最小尺寸面突然受載,在這種情況下,結構的動力效應主要表現為結構的塑性變形隨時間變化,這類問題通常稱為結構的塑性動力回響問題。(見塑性動力學)
粘塑性理論
在傳統的塑性力學中,並不考慮粘性效應。實驗結果表明,金屬、土壤或混凝土的粘性效應都很明顯。考慮粘性效應才能夠解釋變形速度變化對塑性變形的影響。最早研究粘塑性體並給出簡單力學模型的是E.C.賓厄姆,他的力學模型實際上是理想剛塑性體和牛頓流體的組合。目前粘塑性理論在結構的強度和剛度問題中,在塑性動力學中都有廣泛套用。(見
粘塑性理論)
結構的塑性穩定性問題
細長桿件或薄壁結構在壓力下處於平衡狀態,如果受到外界的微小擾動,桿件或結構就可能出現失穩的問題。若失穩前結構處於彈性平衡狀態,則屬於塑性穩定性問題。隨著輕質材料的廣泛使用,最佳化設計的進展,塑性穩定性問題日益增多。在這類問題中平衡的分支點和結構的失穩點並不一致。另外,由於材料在塑性拉伸變形情形下會發生局部的頸縮現象,頸縮處應力的迅速增長也會使結構失穩,這種現象稱為拉伸失穩,是進入塑性階段後所特有的失穩形式。
求解方法
靜定法
求解簡單彈塑性問題的方法。由於所求的各未知量的數目和已知
方程式的數目相同,套用平衡方程和屈服條件便能將問題中的各未知量找出。
滑移線法
適用於求解塑性平面應變問題,可找出變形體中各點的應力分量和所對應的位移分量
界限法
一個有實用價值的方法,又稱上、下限法。上限法採用外力功等於內部耗散能以及結構的幾何條件求塑性極限載荷,其值比完全解的塑性極限載荷大;下限法則用平衡條件、屈服條件以及力的邊界條件求塑性極限載荷,其值比完全解的塑性極限載荷小
主應力法
在屈服條件中不考慮剪應力的貢獻,並假定沿某一個軸主應力的分布是均勻的。用此法能獲得各應力分量的分布規律。
參數方程法
使用米澤斯屈服條件時,可將滿足屈服條件的參數方程代入平衡方程進行求解。
加權殘量法
一種求解微分方程近似解的數學方法。其要點是:先假設一個試
函式作為近似解,將其代入要求解的
控制方程和邊界條件;該函式一般不能完全滿足這些條件,因而出現誤差即殘量;選擇一定的
權函式與殘量相乘,列出在解域內消滅殘量的
代數方程,就可把求解微分方程轉化為求解代數方程的數值計算問題,從而得出近似解。
有限元法
常用的有彈塑性有限元和剛塑性有限元法,可得到變形體內的應力和應變分布規律。
主要套用
①結構的塑性極限分析和安定分析,對梁、桁架、剛架、拱、排架、圓板、矩形極、柱殼、球殼、錐殼、組合殼等都已獲得完全解。
②構件的塑性極限分析和安定分析,已求出各種帶有缺口、槽、孔的受拉、受彎、受扭軸和構件的塑性極限載荷。
③金屬板料成形,包括深沖、翻邊、擴口、縮口等工藝。
④金屬塊體成形,包括鐓粗、拉拔、擠壓、鍛造等工藝。
⑤金屬軋制,金屬材料在兩個反向旋轉的軋輥間通過,並產生塑性變形。
⑥塑性動力回響和
塑性波,在防護工程、
地震工程、穿甲和侵徹,高速成形,超高速撞擊、爆炸工程等方面都有重要套用。
⑦自緊技術,通過使結構產生有益的殘餘應力,以增強厚壁圓筒彈性強度和延長
疲勞壽命。
⑧在岩土力學中,用以研究地基承載能力、
邊坡穩定性、擋土牆的作用和煤柱的承載能力。
⑨用以研究估算和消除殘餘應力的方法。
由於傳統的塑性力學只適用與金屬塑性範圍,特別是硬金屬,當套用於岩石,土壤和混凝土等材料時,往往需要對其一些基本概念作修正,既有了廣義塑性力學的發展。廣義塑性力學放棄了這些假設,採用了分量理論,由固體力學原理直接導出塑性公式,它既適用於岩土材料,也適用於金屬。
上面主要介紹的是從
巨觀角度,以實驗為基礎唯象的研究
塑性變形。在細觀尺度,已經建立
細觀力學,其主要研究目的是從材料物理理論(
位錯、晶體範性、界面等)出發,建立細觀結構與力學性質之間的
定量關係。
細觀力學對經典
連續介質力學理論框架加以改造,引入表征材料細觀結構的損傷的物理或
幾何量,確定其演化方程。同時發展由細觀向
巨觀過度的均勻化方法,建立細觀結構、內部
缺陷與巨觀力學性能之間的
定量關係。從而在細觀尺度上形成一套新的理論框架。
細觀力學中與
塑性變形相關的部分稱塑性細觀力學。相對傳統塑性力學的小變形分析,有關塑性大變形的分析李國琛和M.耶納著《塑性大應變微結構力學》
發展簡史
塑性力學作為固體力學的一個重要分支,其發展的歷史雖然可以追溯到
18世紀的70年代,但真得到充分發展並日臻成熟的是在
20世紀的40年代和50年代初。特別是理想塑性理論,這時已達到成熟並開始在工程實踐中得到套用的階段。塑性變形現象發現較早,然而對它進行力學研究,是從1773年庫侖Coulomb土壤壓力理論,提出土的屈服條件開始的。
H.Tresca於1864年對金屬材料提出了最大
剪應力屈服條件。隨後聖維南於1870年提出在平面情況下理想剛塑性的
應力-應變關係,他假設最大
剪應力方向和最大
剪應變率方向一致,並解出柱體中發生部分塑性變形的扭轉和彎曲問題以及厚壁筒受內壓的問題。Levy於1871年將塑性
應力-應變關係推廣到三維情況。1900年格斯特通過薄管的聯合拉伸和內壓試驗,初步證實最大
剪應力屈服條件。
此後20年內進行了許多類似實驗,提出多種屈服條件,其中最有意義的是Mises於1913年從
數學簡化的要求出發提出的屈服條件(後稱米澤斯條件)。米澤斯還獨立地提出和Levy一致的塑性
應力-應變關係(後稱為Levy-Mises
本構關係)。泰勒於1913年,Lode於1926年為探索應力-應變關係所作的
實驗都證明,萊維-米澤斯本構關係是真實情況的一級近似。
為更好地
擬合實驗結果,羅伊斯於1930年在普朗特的啟示下,提出包括彈性應變部分的三維塑性應力-應變關係。至此,塑性增量理論初步建立。但當時增量理論用在解具體問題方面還有不少困難。早在1924年亨奇就提出了塑性
全量理論,由於便於套用,曾被納戴等人,特別是伊柳辛等蘇聯學者用來解決大量實際問題。
雖然塑性
全量理論在理論上不適用於複雜的應力變化歷程,但是計算結果卻與板的失穩實驗結果很接近。為此在1950年前後展開了塑性增量理論和塑性
全量理論的辯論,促使從更根本的理論基礎上對兩種理論進行探討。另外,在強化規律的研究方面,除等向強化模型外,普拉格又提出隨動強化等模型。電子計算機的發展,為塑性力學的研究和套用開展了廣闊的前景,特別是促進了有限單元法的套用。1960年,Argyris提出初始荷載法可作為有限單元發解彈塑性問題的基礎。自此理想塑性的塑性力學已經達到定型的階段,而具有加工硬化的塑性力學至今仍是在發展中研究課題。
20世紀60年代以後,有限元法的發展,提供恰當的本構關係已成為解決問題的關鍵。所以70年代關於塑性
本構關係的研究十分活躍,主要從
巨觀與微觀的結合,從不
可逆過程熱力學以及從
理性力學等方面進行研究。
在實驗分析方面,也開始運用光塑性法、
雲紋法、
散斑干涉法等能測量大變形的手段。另外,由於出現岩石類材料的塑性力學問題,所以塑性體積應變以及材料的各向異性、非均勻性、彈塑性耦合、應變弱化的非穩定材料等問題正在研究之中。