在信號與系統中,對周期信號f(t)進行指數傅立葉變換,得到的係數是復振幅,描述復振幅和n次諧波頻率之間的關係的圖形是複數振幅譜圖。在複數振幅譜圖中,負頻率的出現全是數學運算的結果,並無任何物理意義。
基本介紹
- 中文名:復振幅
- 外文名:Complex amplitude
- 歸屬學科:信號與系統
- 通過:指數傅立葉變換得到
- 相關:復振幅頻譜
- 套用:信號處理
定義


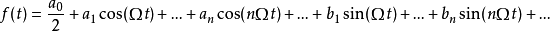






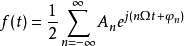





頻譜
幅度譜

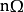

相位譜

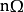
複數振幅譜

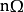
例題
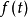


在信號與系統中,對周期信號f(t)進行指數傅立葉變換,得到的係數是復振幅,描述復振幅和n次諧波頻率之間的關係的圖形是複數振幅譜圖。在複數振幅譜圖中,負頻率的出現全是數學運算的結果,並無任何物理意義。


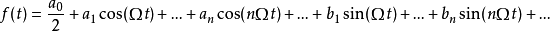






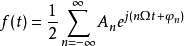






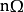


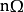

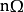
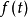


在信號與系統中,對周期信號f(t)進行指數傅立葉變換,得到的係數是復振幅,描述復振幅和n次諧波頻率之間的關係的圖形是複數振幅譜圖。在複數振幅譜圖中,負頻率的...
振幅調變也可簡稱為調幅,是在電子通信中使用的一種調製方法,最常用於無線電載波傳輸信息。在幅度調製中,載波的幅度(信號強度)是與所傳送的波形成比例變化的。例如...
對於所討論的正弦光柵,單位衍射產生的復振幅為該式記為式(2),其中略去了積分號前的常係數和二次相位因子,它們對所求的強度分布沒有影響。將式(1)代入式(2)...
相位共軛波是與原始波有相同的頻率,且其空間復振幅為原始波的空間復振幅的復共軛。能對光波實現相位復共軛作用的光學系統稱相位共軛鏡。...
其中、是兩列波各自獨立的光強,而是干涉項。 我們用、表示兩列波的復振幅,則干涉項中可以寫為前兩項對時間取平均值仍然為零,從而干涉項對光強的貢獻為...
衍射屏是能使波前上復振幅發生改變的物的統稱,可以是反射物,也可以是透射物。...... 衍射屏是能使波前上復振幅發生改變的物的統稱,可以是反射物,也可以是透射...
在製作計算全息圖時只需要物波函式的復振幅分布編碼成全息圖的透過率函式。通過繪圖儀和光學縮版就得到像計算全息圖。計算傅立葉變換全息圖:被記錄的複數波面是物...
在光學上巴俾涅原理用於論述兩個互補屏在衍射場中某點單獨產生的復振幅之和等於光波自由傳播時該點的復振幅。巴俾涅原理[1] 給出的三個場之關係是復振幅關係,...
相位共軛波是在振幅、 相位(即波陣面)及偏振態三個方面互為時間反演的光波。 在數學上相當於給光電場作用一個算符, 使其復振幅轉變為它的復共軛, 並因此而...
