P/NP問題是在理論信息學中計算複雜度理論領域裡至今沒有解決的問題，它被“克雷數學研究所”（Clay Mathematics Institute, 簡稱CMI）在千禧年大獎難題中收錄。 P/NP問題中包含了複雜度類P與NP的關係。1971年史提芬·古克(Stephen A. Cook) 和 Leonid Levin 相對獨立的提出了下面的問題，即是否兩個複雜度類P和NP是恆等的（P=NP?）。
基本介紹
- 中文名：P/NP問題
- 收錄：克雷數學研究所
- 時間：1971年
- 含義：個複雜度類P和NP是恆等的
P/NP問題,P和NP,NP完全,P容易處理嗎,科學家的理論,學術定義,證明的難度,多項時間算法,更難的問題,邏輯表述,花絮,最新訊息,
P/NP問題
P和NP
複雜度類P包含所有那些可以由一個確定型圖靈機在多項式表達的時間內解決的問題；類NP由所有其肯定解可以在給定正確信息的多項式時間內驗證的決定問題組成，或者等效的說，那些解可以在非確定圖靈機上在多項式時間內找出的問題的集合。很可能，計算理論最大的未解決問題就是關於這兩類的關係的:
P和NP相等嗎?
在2002年對於100研究者的調查，61人相信答案是否定的，9個相信答案是肯定的，22個不確定，而8個相信該問題可能所接受的公理獨立，所以不可能證明或證否。[1] 所以P-NP問題也是Clay研究所的七個百萬美元大獎問題之一。
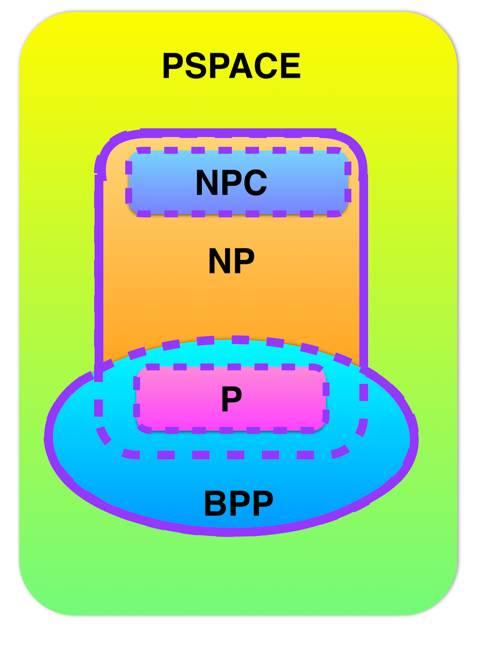
NP-完全問題(或者叫NPC)的集合在這個討論中有重大作用，它們可以大致的被描述為那些在NP中最不像在P中的。(確切定義細節請參看NP-完全)理論計算機科學家現在相信P, NP,和NPC類之間的關係如圖中所示，其中P和NPC類不交。
假設P ≠ NP的複雜度類的圖解.如P = NP則三個類相同.本質上，P = NP問題問道：如果是/不是問題的正面答案可以很快驗證，其答案是否也可以很快計算？這裡有一個給你找點這個問題的感覺的例子。給定一個大數Y,我們可以問Y是否是複合數。例如，我們可能問53308290611是否有非平凡的因子。回答是肯定的，雖然手工找出一個因子很麻煩。從另一個方面講，如果有人聲稱答案是"對，因為224737可以整除53308290611",則我們可以很快用一個除法來驗證。驗證一個數是除數比首先找出除數來簡單得多。用於驗證一個正面答案所需的信息也稱為證書。所以我們的結論是，給定 正確的證書，問題的正面答案可以很快的(也就是，在多項式時間內)驗證，而這就是這個問題屬於NP的原因。雖然這個特定的問題，證明為也在P類中(參看下面的關於"質數在P中"的參考),這一點也不明顯，而且有很多類似的問題相信不屬於類P。
限制到是/不是問題並沒有改變問題；即使我們允許更複雜的答案，最後的問題(是否FP = FNP)是等價的。
NP完全
P容易處理嗎
上面所有的討論假設了P表示“容易”而“不在P中”表示“困難”。這是一個在複雜度理論中常見而且有一定準確性的假設，它在實踐中卻不總是真的，原因包括如下幾點：
它忽略了常數因子。一個需要101000n時間的問題是屬於P的（它是線性時間的），但是事實上完全無法處理。一個需要10-100002n時間的問題不是在P中的（它是指數時間的），但是對於n 取值直到幾千時還是很容易處理的。
它忽略了指數的大小。一個時間複雜度n1000屬於P，但是很難對付。已經證明在P中存在需要任意大的指數的問題（參看時間等級定理）。一個時間複雜度2n/1000的問題不屬於P，但對與n直到幾千還是容易應對的。
它只考慮了最壞情況的複雜度。可能現實世界中的有些問題在多數時候可以在時間n中解決，但是很偶爾你會看到需要時間2n的特例。這個問題可能有一個多項式的平均時間，但最壞情況是指數式的，所以該問題不屬於P。
它只考慮確定性解。可能有一個問題你可以很快解決如果你可以接受出現一點誤差的可能，但是確保正確的答案會難得多。這個問題不會屬於P，雖然事實上它可以很快求解。這實際上是解決屬於NP而還不知道是否屬於P的問題的一個辦法（參看RP， BPP）。
新的諸如量子電腦這樣的計算模型，可能可以快速的解決一些尚未知道是否屬於P的問題；但是，沒有一個它們已知能夠解決的問題是NP完全的。不過，必須注意到P和NP問題的定義是採用象圖靈機這樣的經典計算模型的屬於表述的。所以，即使一個量子計算機算法被發現能夠有效的解決一個NP完全問題，我們只是有了一個快速解決困難問題的實際方法，而不是數學類P和NP相等的證明。
科學家的理論
多數計算機科學家相信P≠NP。該信念的一個關鍵原因是經過數十年對這些問題的研究，沒有人能夠發現一個NP完全問題的多項式時間算法。而且，人們早在NP完全的概念出現前就開始尋求這些算法了（Karp的21個NP完全問題，在最早發現的一批中，有所有著名的已經存在的問題]]）。進一步地，P = NP這樣的結果會導出很多驚人的結果，那些結果現在被相信是不成立的，例如NP = 余NP和P = PH。
也有這樣論證的：問題較難求解(NP)但容易驗證(P)，這和我們日常經驗是相符的。
從另一方面講，某些研究者認為我們過於相信P ≠ NP，而應該也去尋找P = NP的證明。例如，2002年中有這樣的聲明：
傾向P≠NP的主要論據是在窮盡搜尋的領域完全沒有本質進展。也就是說，以我的觀點，一個很弱的論據。算法的空間是很大的，而我們只是在開始探索的起點。[ . . . ] 費馬最後定理的解決也顯示非常簡單的[sic]問題可能只有用非常深刻的理論才能解決。
— Moshe Vardi，萊斯大學
過分依賴某種投機不是規劃研究的一個好的導引。我們必須總是嘗試每個問題的兩個方向。偏見可能導致著名的數學家無法解決答案和他們的預計相反的著名問題，雖然他們發展了所有所需的方法。
— Anil Nerode, 康奈爾大學
學術定義
假設有一個算法A(w,C)取兩個參數，一個串w，也就是我們的決定問題的輸入串，而另一個串C是“建議證明”，並且使得A在最多n^k步之內產生“是/否”答案（其中n是w的長度而k不依賴於w）。進一步假設
w是一個答案為“是”的例子，若且唯若，存在C使得A(w,C)返回“是”。
則我們稱這個問題可以在非決定性多項式時間內解決，且將它放入NP類。我們把算法A作為一個所建議的證明的檢驗器，它運行足夠快。（注意縮寫NP代表“Non-deterministic（非確定性）Polynomial（多項式）”而不是代表“Non-Polynomial（非多項式）。）
證明的難度
雖然百萬美元的獎金和大量投入巨大卻沒有實質性結果的研究足以顯示該問題是困難的，還有一些形式化的結果證明為什麼該問題可能很難解決。
最常被引用的結果之一設計神喻。假想你有一個魔法機器可以解決單個問題，例如決定一個給定的數字是否為質數，但可以瞬間解決這個問題。我們的新問題是，若我們被允許任意利用這個機器，是否存在我們可以在多項式時間內驗證但無法在多項式時間內解決的問題？結果是，依賴於機器能解決的問題，P = NP和P ≠ NP二者都可以證明。這個結論的後果是，任何可以修改來證明該機器的存在性的結果不能解決問題。不幸的是，幾乎所有經典的方法和大部分已知的方法可以這樣修改（我們稱它們在相對化）。
如果這還不算太糟的話，1993年Razborov和Rudich證明的一個結果表明，給定一個特定的可信的假設，在某種意義下“自然”的證明不能解決P = NP問題。[3] 這表明一些現在似乎最有希望的方法不太可能成功。隨著更多這類的定理得到證明，該定理的可能證明有越來越多的陷阱要規避。
這實際上也是為什麼NP完全問題有用的原因：若有一個多項式時間算法，或者沒有一個這樣的算法，對於NP完全問題存在，這將用一種相信不被上述結果排除在外的方法來解決P = NP問題。
多項時間算法
沒人知道多項式時間算法對於NP完全問題是否存在。但是如果這樣的算法存在，我們已經知道其中的一些了！例如，下面的算法正確的接受了一個NP完全語言，但是沒人知道通常它需要多久運行。它是一個多項式時間算法若且唯若P = NP。
// 接受NP完全語言的一個算法子集和。
//
// 這是一個多項式時間算法若且唯若P=NP。
//
// “多項式時間”表示它在多項式時間內返回“是”，若
// 結果是“是”，否則永遠運行。
//
// 輸入：S = 一個自然數的有限集
// 輸出："是" 如果某個S的子集加起來等於0。
// 否則，它永遠運行沒有輸出。
// 注意: "程式數P" 是你將一個整數P寫為二進制，然後
// 將位串考慮為一個程式。
// 每個可能的程式都可以這樣產生，
// 雖然多數什麼也不做因為有語法錯誤。
//
FOR N = 1...infinity
FOR P = 1...N
以S為輸入運行程式數P N步
IF 程式輸出一個不同的整數的列表
AND 所有整數都在S中
AND 整數的和為0
THEN
OUTPUT "是" 並 停機
若P = NP，則這是一個接受一個NP完全語言的多項式時間算法。“接受”表示它在多項式時間內給出“是”的答案，但允許在答案是“否”的時候永遠運行。
可能我們想要“解決”子集和問題，而不是僅僅“接受”子集和語言。這表示我們想要它總是停機並返回一個“是”或“否”的答案。是否存在任何可能在多項式時間內解決這個問題的算法？沒有人知道。但是如果這樣的算法存在，那么我們已經知道其中的一些了！只要將上面的算法中的IF語句替換成下面的語句：
IF 程式輸出一個完整的數學證明
AND 證明的每一步合法
AND 結論是S確實有（或者沒有）一個和為0的子集
THEN
OUTPUT "是" （或者"不是"如果那被證明了）並停機
更難的問題
雖然是否P=NP還是未知的，在P之外的問題是已經知道存在的。尋找西洋棋或圍棋最佳走法（在n乘n棋盤上）是指數時間完全的。因為可以證明P ≠ EXPTIME（指數時間），這些問題位於P之外，所以需要比多項式時間更多的時間。判定Presburger算術中的命題是否為真的問題更加困難。Fischer和Rabin於1974年證明每個決定Presburger命題的真偽性的算法有最少2^(2^(cn))的運行時間，c為某個常數。這裡，n是Presburger命題的長度。因此，該命題已知需要比指數時間更多的運行時間。不可判定問題是更加困難的，例如停機問題。它們無法在任何給定時間內解決。
邏輯表述
P=NP問題可以用邏輯命題的特定類的可表達性的術語來重新表述。所有P中的語言可以用一階邏輯加上最小不動點操作（實際上，這允許了遞歸函式的定義）來表達。類似地，NP是可以用存在性二階邏輯來表達—也就是，在關係、函式、和子集上排除了全域量詞的二階邏輯。多項式等級，PH中的語言對應與所有的二階邏輯。這樣，“P是NP的真子集嗎”這樣的問題可以表述為“是否存在性二階邏輯能夠表達帶最小不動點操作的一階邏輯的所不能表達的語言？”
花絮
普林斯頓大學計算機系樓將二進制代碼表述的“P=NP?”問題刻進頂樓西面的磚頭上。如果證明了P=NP，磚頭可以很方便的換成表示“P=NP！”。[4]
康奈爾大學的Hubert Chen博士提供了這個玩笑式的P不等於NP的證明：“反證法。設P = NP。令y為一個P = NP的證明。證明y可以用一個合格的計算機科學家在多項式時間內驗證，我們認定這樣的科學家的存在性為真。但是，因為P = NP，該證明y可以在多項式時間內由這樣的科學家發現。但是這樣的發現還沒有發生（雖然這樣的科學家試圖發現這樣的一個證明），我們得到矛盾。
最新訊息
公元2010年：
8 月 6 日，HP LAB的 Vinay Deolalikar 教授宣布證明了P!=NP，證明文章已經傳送到該問題各相關領域專家手中，等待檢驗，在他的主頁上，證明過程已經公布（PDF格式共103頁）。
8 月 8 日，Lipton 在部落格上討論了這篇論文，給出了略顯樂觀的評價：這是一個值得認真對待的證明。這篇文章引來大量嚴肅的學術性回復，大多來自業內人士，各方看法不一。
8 月 9 日，Lipton 在參考各方反應的基礎上同 Ken Regan 合寫了一篇新的部落格文章，指出了 Deolalikar 證明思路中的一些重大漏洞，對它的整體評價口吻較前日明顯低調了許多。
同日，因為 Lipton 部落格文章後面大量有價值的評論值得梳理，Venkatasubramanian 建立了一個可以被公眾編輯的 Google Docs 文檔以整理這些討論。翌日，在陶哲軒的幫助下，該文檔被轉換成一個 wiki 架構的頁面。
8 月 10 日，Lipton 寫了新的部落格文章，試圖將各方討論的結果以更清晰的方式呈現出來。這篇文章繼續成為各方討論的平台，更多學術上的批評開始浮出水面。更多科學家參與了部落格評論以及 wiki 頁面的編輯。同日，Deolalikar 在自己的網站上撤下了論文初稿的連結，稍後放上了新一稿。
8 月 11 日，Lipton 貼出了 Deolalikar 對一部分學術質疑的答覆。Vinay Deolalikar 貼出了論文的第三稿。
同一日，在學術討論之外，各方對事態發展的速度和形式本身開始進行反思。Lipton 和陶哲軒等人認為一個藉助網際網路平台被良好組織起來的討論可以產生很好的效果，無論對於 Deolalikar 改進他的證明還是對於推進人們關於 P/NP 問題本身的了解都有益處。而另一些科學家，以 Impagliazzo 為代表，認為網路討論導致了人們反應過度，浪費了太多本可以從事其它研究的時間。這一論點引起了大量爭論。
8 月 12 日，Lipton 貼出了一封來自 Neil Immerman 的信，指出了兩個此前未被認真討論的漏洞。
8 月 13 日，Deolalikar 貼出了一篇關於自己的證明的解釋性文檔。
8 月 14 日，在很多科學家的共同討論中，人們逐漸釐清 Deolalikar 的論文的根本問題在於把兩個沒有在論文中被嚴格定義出來的直觀概念混淆在一起，從而做出了不完善的論證。
8 月 15 日，Lipton 貼出了他對於一周以來討論的總結。人們關於論文的看法——即證明不能成立——已經趨於穩定（當然這不能排除大家都同時犯了錯誤的可能性），隨後的發言越來越多地集中於更抽象的層面，並且至今仍在繼續。
