在計算複雜性理論，一個被稱為線性時間或 Ο（n）時間的算法，表示此算法解題所需時間正比於輸入資料的大小，通常以n表示。換句話說，執行時間與輸入資料大小為線性比例。例如將一列數字加總的所需時間，正比於串列的長度。
基本介紹
- 中文名：線性時間
- 別稱：線性時間或 Ο（n）時間的算法
- 套用學科：線性比例
- 適用領域範圍：數學
- 適用領域範圍：時間與輸入資料大小為線性比例
簡介,內容,常量時間,
簡介
在計算複雜性理論，一個被稱為線性時間或 Ο（n）時間的算法，表示此算法解題所需時間正比於輸入資料的大小，通常以n表示。換句話說，執行時間與輸入資料大小為線性比例。例如將一列數字加總的所需時間，正比於串列的長度。
然而實際情況常有差距，真實的執行時間很可能與預期的比率相差甚大，尤其在n的值很小時。在技術討論時，在足夠大的量n之下算法的執行時間從an到bn（a、b為正實數）時，就可稱線性時間。詳情請看大O符號。
內容
達到線性時間的執行效能通常是一個算法的最佳目標。很多學者研究並創造了許多接近線性或更佳的算法，包括了軟體或硬體方面的研究。硬體方面，藉由諸如平行運算的硬體架構，使得某些數學認為無法在標準計算模型下達到線性時間的算法，如今都可以線上性時間內執行完畢。例如內容可定址記憶體（Content-addressable memory）。
某些排序算法可以在特殊的數據結構及排列下擁有線性時間的效率。但在一般情況下以比較元素大小來排序的算法，最多只能到達Ο（nlog（n））。最低限度複雜性的證明已被小O符號含括；通用排序算法被認為是Ω（n log（n））。另外，要找到一個集合中最大的元素是 Ω（n），因為算法必須至少比較過（n-1）次才能找到最大元素。
任何必須依賴全部輸入內容才能得解的問題，它最少也得要線性時間才能得解，因為它至少得花線性時間來讀取輸入資料。
常量時間
常量時間記為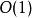
（採用大O符號）。數字1可以替換為任意常數。
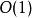
舉例：
- 想在“訪問數組上的元素”的問題上達到常量時間，只要以元素的序號訪問即可。
- 然而“在數組上搜尋最小值”並不是一個常量時間問題，因為這需要掃描數組上的每一個元素以尋找最小值及其位置，一般需要O(n)次訪問。
