n階行列式等於所有取自不同行不同列的n個元素的乘積的代數和,逆序數為偶數時帶正號,逆序數為奇數時帶負號,共有n!項。
基本介紹
- 中文名:n階行列式
- 外文名:n-order determinant
- 性質:有n!項
- 本質:數
- 計算方法:對角線法則、定義法、性質法等
- 所屬領域:線性代數
簡介
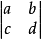
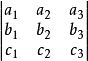
定義


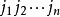
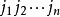
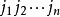



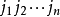
n階行列式的性質
n階行列式的計算




范德蒙德行列式


n階行列式等於所有取自不同行不同列的n個元素的乘積的代數和,逆序數為偶數時帶正號,逆序數為奇數時帶負號,共有n!項。
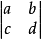
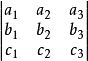


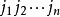
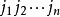
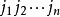



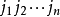





n階行列式等於所有取自不同行不同列的n個元素的乘積的代數和,逆序數為偶數時帶正號,逆序數為奇數時帶負號,共有n!項。...
①行列式A中某行(或列)用同一數k乘,其結果等於kA。②行列式A等於其轉置行列式AT(AT的第i行為A的第i列)。③若n階行列式|αij|中某行(或列);行列式則|α...
行列式依列展開(expansion of a determinant by a column)是計算行列式的一種方法,設a1j,a2j,…,anj (1≤j≤n)為n階行列式D=|aij|的任意一列中的元素,...
行列式依行展開(expansion of a determinant by a row)是計算行列式的一種方法,設ai1,ai2,…,ain (1≤i≤n)為n階行列式D=|aij|的任意一行中的元素,而Ai...
矩陣行列式是指矩陣的全部元素構成的行列式,設A=(aij)是數域P上的一個n階矩陣,則所有A=(aij)中的元素組成的行列式稱為矩陣A的行列式,記為|A|或det(A)。若...
如右圖利用加減消元法,為了容易記住其求解公式,但要記住這個求解公式是很困難的,因此引入三階行列式的概念。記稱左式的左邊為三階行列式,右邊的式子為三階行列式的...
一個e階的范德蒙行列式由e個數c₁,c₂,…,cₑ決定,它的第1行全部都是1,也可以認為是c₁,c₂,…,cₑ各個數的0次冪,它的第2行就是c₁,c...
計算行列式通常用降階法,但有時也可反其道而行之,將它的階數放大,增加一行一列,使升階後的行列式與原行列式相等,且易於計算(即適當選擇所增加的行列元素,使下...
主對角線(從左上角到右下角這條對角線)下方的元素全為零的行列式稱為上三角行列式。一個n階行列式若能通過變換,化為上三角行列式,則計算該行列式就很容易了。....
帶形行列式是一種特殊形狀的行列式,形如帶狀的n階行列式稱為帶形行列式,其中主對角線上的元素全是a,與主對角線平行的兩條線上的元素分別全為b和c,其餘的元素...
在n階行列式中,把元素aₒₑi所在的第o行和第e列划去後,留下來的n-1階行列式叫做元素aₒₑi的餘子式,記作Mₒₑ,將餘子式Mₒₑ再乘以-1的...
在n 階行列式中,選取行號(如 1、3、7行),再選取與行號相同的列號(1、3、7 列),則行數和列數都為i個的行列式即為n階行列式的i階主子式,也可以說由上述...
行列式的階越低越容易計算,於是很自然地提出,能否把高階行列式轉換為低階行列式來計算,為此,引入了餘子式和代數餘子式的概念。在n階行列式中,把所在的第i行與...
在一個n階方陣(或是n階行列式)中,從左上角到右下角這一斜線上的n 個元素的位置,叫做n 階方陣(或行列式)的主對角線。...
用克萊姆法則求解方程組實際上相當於用逆矩陣的方法求解線性方程組,它建立線性方程組的解與其係數和常數間的關係,但由於求解時要計算n+1個n階行列式,其工作量常常...
順序主子式是取n階方陣的部分元素化為行列式形式。方陣的第k階行列式是由該方陣的前k行和k列元素組成。對於n階方陣A,其共有n階順序主子式。通過計算方陣A的...
(1)當方程組的方程個數與未知數的個數不一致時,或者當方程組係數的行列式等於零時,克萊姆法則失效。(2)運算量較大,求解一個N階線性方程組要計算N+1個N階...
給定一個數域F,則稱數域Fn上的規範對稱n重線性函式叫做n階積和式(permanent)。 [2] 這和n階行列式對比:給定一個數域F,則稱數域Fn上的規範反對稱n重線性...
1?1?2二階與三階行列式1?1?3n階行列式習題1?11?2行列式的性質習題1?21?3行列式按行(列)展開習題1?3複習題一第2章矩陣2?1矩陣的基本概念...
2.3方陣的行列式 2.3.1n階行列式的定義 2.3.2行列式的性質 2.3.3行列式的計算 2.4求解線性方程組的Cramer法則 2.5矩陣的分塊技巧 2.5.1分塊矩陣的定義 2.5...
