基本介紹
- 中文名:Jordan標準型
- 外文名:Jordan standard form
- 特點1:主對角線上元素為特徵值
- 特點2:主對角線上方相鄰斜對角線為1
- 工具:初等因子理論
- 套用學科:高等數學
定義

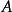


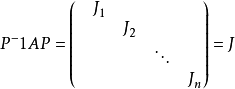

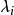
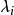

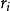

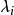
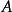
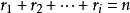


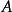
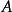

實例
Jordan陣
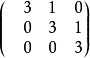



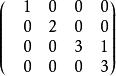
非Jordan陣

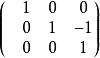
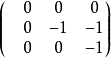


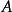


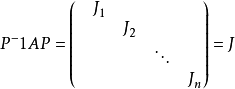

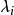
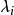

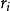

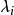
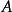
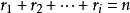


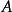
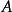

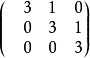



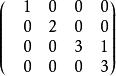

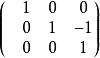
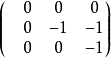
每個n階的複數矩陣A都與一個若爾當形矩陣相似,這個若爾當形矩陣除去其中若爾當塊的排列次序是被矩陣A唯一確定的,它稱為矩陣A的若爾當標準型。首先,Jordan標準型...
Jordan標準型的定義定義:由主對角線為特徵值,次對角線為1的約旦塊按對角排列組成的矩陣稱為Jordan形矩陣,而主對角線上的小塊方陣Ji稱為Jordan塊·...
該書共分12章,主要介紹線性空間與線性變換、內積空間與等距變換、特徵值與特徵向量、λ-矩陣與Jordan標準形、特殊矩陣、矩陣分析初步、矩陣函式的套用、矩陣的分解、...
(2)當A不能與對角陣相似時,則A必與Jordan標準型相似,設最後矩陣函式利用最小多項式 用最小多項式求矩陣函式 的具體步驟如下:第一步 計算矩陣A的最小多項式 ,...
從而引進線性空間、線性不等式和它上面的線性變換,以及求複方陣的Jordan標準形的代數理論和幾何解釋,Jordan標準形的套用,它包含了方陣函式和方陣在復相似下的標準型...
“高等代數”,“矩陣理論”與“近世代數”的基本內容;即:多項式,行列式,矩陣及其各種運算,線性方程組,二次型,相似矩陣,線性空間,線性變換,Jordan標準形,矩陣函式,...
Jordan標準形,證明了Schur三角化定理與Cayley-Hamilton定理,給出了矩陣在相似變換下的最簡形式即Jordan標準形,討論了特徵值估計的蓋爾圓盤定理,介紹了特徵值與特徵...
代數表示論就是研究一個給定的Artin代數是有限型還是無限型。若是有限型,確定其全體不可分解模;若是無限型,給出模的分布情況。我們大家所熟悉的Jordan標準型就...
內容包括向量、矩陣、行列式、秩、逆矩陣、線性方程、LU分解、特徵值、對角化、Jordan標準型、特徵值算法等。 [1] 程式設計師的數學3作者簡介 編輯 ...
3.3.3 矩陣Jordan標準形§3.4 方陣的最小多項式3.4.1 方陣的化零多項式3.4.2 最小多項式3.4.3 最小多項式與方陣相似於對角矩陣的條件...
下冊(第六章至第十二章)包括三方面內容:一是帶度量的線性空間及Jordan標準形,這是線性代數較深入的知識;二是有理整數環及一元、多元多項式環;三是選講內容:n維...
8.3.3 求λ-矩陣的Smith標準形、不變因子和初等因子8.3.4 λ-矩陣等價的判定與證明8.3.5 相似矩陣的判定與證明8.3.6 求矩陣的Jordan標準形和有理標準形8.3.7...
二、Jordan塊的性質及其套用8.4 Jordan標準形的相似過渡陣的求法8.5 最小多項式一、最小多項式及其性質二、最小多項式的求法三、最小多項式的套用(實例)...
§5.2 矩陣相似對角化§5.3 Jordan標準形介紹習題五第六章 二次型§6.1 二次型及其矩陣表示§6.2 二次型的標準形§6.3 用正交變換化二次型為標準形...
8若爾當(Jordan)標準形介紹 9最小多項式 習題 補充題 第八章λ—矩陣 1λ—矩陣 2λ—矩陣在初等變換下的標準形 3不變因子 4矩陣相似的條件 5...
