1-2+3-4+…

在數學中，1-2+3-4+…表示以由小到大的逐次正整數，依序加後又減、減後又加，如此反覆所構成的無窮級數，為一交錯級數。若使用Σ符號表示前m項之和，可寫作：

此無窮級數發散，即其部分和的序列（1, −1, 2, −2, …）不會趨近於任一有窮極限，可等價地認為1 − 2 + 3 − 4 + …不存在和。

不過，在18世紀中期，萊昂哈德·歐拉寫出了一個他承認為悖論的等式：

該等式的嚴密解釋在很久以後才出現。1890年初，恩納斯托·切薩羅、埃米爾·博雷爾與其他一些數學家研究出了定義良好的方法，來求發散級數的廣義和——其中包含了對歐拉結果的新解釋。這些求和法大部分可簡單地賦予1 − 2 + 3 − 4 + …的“和”⁄4。切薩羅求和是少數幾種不能計算出1 − 2 + 3 − 4 + …之和的方法，因為此級數求和需要某個略強的方法——譬如阿貝耳求和。

級數1 − 2 + 3 − 4 + …與格蘭迪級數1 − 1 + 1 − 1 + …聯繫緊密。歐拉將這兩個級數當作1 − 2 + 3 − 4 + …的特例（其中n為任意自然數），這個級數既直接擴展了他在巴塞爾問題上所做的工作，同時也引出了我們現在所熟知的狄利克雷η函式和黎曼ζ函式。

基本介紹

• 中文名：1 ? 2 + 3 ? 4 + …
• 組成：部分和的序列
• 發現者：埃米爾·博雷爾
• 類型：數學

發散性

級數項（1, −2, 3, −4, …）沒有趨近；因此可通過項測試來確定1 − 2 + 3 − 4 + …發散。作為後文的參考，此方法也常被用於從基礎級上預見發散。從定義可知，無窮級數的收斂或發散是由其部分和的收斂或發散確定的，1 − 2 + 3 − 4 + …的部分和為：

• 1 = 1,
• 1 − 2 = −1,
• 1 − 2 + 3 = 2,
• 1 − 2 + 3 − 4 = −2,
• 1 − 2 + 3 − 4 + 5 = 3,
• 1 − 2 + 3 − 4 + 5 − 6 = −3,
• …

此部分和序列的一個顯著特點是每個整數都出現了一次——如果將空部分和計入還包括0——因此其可數集為整數集。很明顯的，不可能讓變化的結果收斂到一個確定的數，因此1 − 2 + 3 − 4 + …發散。

求和的啟發

穩定性與線性

由於各項 1, −2, 3, −4, 5, −6, … 以一種簡單模式排列，級數1 − 2 + 3 − 4 + …可表示為它自己的變換形式（概略的說法），而因此所得的方程解取得一數值。暫時假設寫作s = 1 − 2 + 3 − 4 + …有意義——其中的s為常數，然後再處理的問題：

因此，如圖1所示。

複製4份 1 − 2 + 3 − 4 + …，僅使用移動與項項相加，結果為1。左右兩邊的兩個1 − 2 + 3 − 4 + …副本相互抵消，並得出1 − 1 + 1 − 1 + …。

儘管1 − 2 + 3 − 4 + …沒有通常意義的和，等式s = 1 − 2 + 3 − 4 + … =卻可被賦予另外一種意義。離散級數之“和”的一種普遍定義被稱為一種求和法或可和法——對所有可能級數的一些子集求和。有許多種不同的方法（部分將在下文中出現），這些方法有著與常數求和所共有的特性。以上的處理實際上都可由下述所證明：給出任意的線形且穩定的可和法，並計算級數1 − 2 + 3 − 4 + …，結果為此外，由於：

圖1 複製4份

故此方法也一定能對格蘭迪級數求和，並得結果為

柯西乘積

1891年，恩納斯托·切薩羅發表了將發散級數嚴密地帶入微積分學的想法，並指出：“已可寫出(1 − 1 + 1 − 1 + …) = 1 − 2 + 3 − 4 + …並斷定兩邊均等於。”對切薩羅而言，這個等式是他前幾年發表的一個定理的套用，該定理也許是歷史上可求和的發散級數的第一個定理。關於此求和法的詳細內容請見下文；其中心思想是1 − 2 + 3 − 4 + …是1 − 1 + 1 − 1 + …對1 − 1 + 1 − 1 + …的柯西乘積。

1 − 2 + 3 − 4 + … 以 1 − 1 + 1 − 1 + … 的二重柯西乘積出現

1 ? 2 + 3 ? 4 + …

兩個無窮級數的柯西乘積可被確定，即使在他們都發散的時候。在 Σa_n= Σb_n= Σ(−1) 的情況下，柯西乘積的項可由有窮對角線求和的方式給出：

積級數為：

這樣一種考慮到兩個級數的柯西乘積與結果的求和法，也能夠求出。由前部分的結果可知，當方法是線形、穩定並考慮到柯西乘積的時候，1 − 1 + 1 − 1 + …與1 − 2 + 3 − 4 + …的可求和之間是等價的。

切薩羅的定理是一個深奧的例子。級數1 − 1 + 1 − 1 + …在最弱的意義上是切薩羅可求和，稱作(C, 1)-可求和，然而1 − 2 + 3 − 4 + …則需要切薩羅的定理的一個更強的形式，表示為(C, 2)-可求和。由於切薩羅的定理的所有形式均為線形且穩定的，所得的值正是此前計算所得的。

特殊方法

切薩羅與赫爾德

關於⁄₄的(H, 2)和的數據

若1 − 2 + 3 − 4 + …的(C, 1)切薩羅和存在，要找到其數值就需要計算該級數部分和的算術平均值。 部分和為：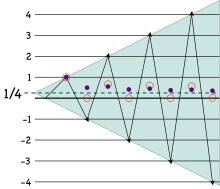

1 ? 2 + 3 ? 4 + …

1, −1, 2, −2, 3, −3, …,

這些部分和的算術平均值為：

1, 0,⁄₃, 0,⁄₅, 0,⁄₇, ….

此平均值序列沒有收斂，因此 1 − 2 + 3 − 4 + … 不是切薩羅可求和。

切薩羅求和有兩種有名的廣義化：讓這些在概念上更簡單的是(H, n)法的序列，其中n為自然數。(H, 1)和為切薩羅求和，更高的方法則重複平均值的計算。在上文中，偶數平均值趨近於⁄₂，奇數平均值則全部等於0，所以平均值的平均值趨近於 0 與⁄₂的平均數，即⁄₄。因此，1 − 2 + 3 − 4 + …是(H, 2)-可求和為⁄₄。

符號“H”代表奧圖·赫爾德。1882年，他第一次證明了被現在數學家們所看作的在阿貝耳求和與(H, n)求和之間的關係；1 − 2 + 3 − 4 + …是第一個例子。⁄₄是1 − 2 + 3 − 4 + …的(H, 2)和這個事實也保證了它是阿貝耳和；這些都將在下文直接予以證明。

另外一個普遍明確的切薩羅求和的廣義化，是(C, n)法的序列。已經證明了(C, n)求和與(H, n)求和均能給出相同的結果，但是它們卻有不同的歷史背景。在1887年，切薩羅已經接近於陳述出(C, n)求和的定義了，但是他只給出了少量的例子。特別的，他在計算1 − 2 + 3 − 4 + …,為⁄₄時所採用的方法可能是(C, n)的另一種描述，但是在當時並沒有對其進行證明。他在1890年正式定義了(C, n)法，以陳述他的定理：一個(C, n)-可求和級數與一個(C, m)-可求和級數的柯西乘積是(C, m + n + 1)-可求和。

阿貝耳求和

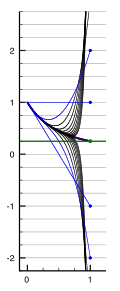
1−2x+3x+…; 1/(1 + x) 的一部分；其極限為1

在一份1749年的報告中，萊昂哈德·歐拉承認了級數發散，但準備用任何方式對其求和：

1 ? 2 + 3 ? 4 + …

……當該級數1 − 2 + 3 − 4 + 5 − 6 …的和為⁄₄時，那肯定出現了悖論。對該級數的100項相加，我們得到了-50，但是，101項的和卻給出+51，這與⁄₄是截然不同的，而且這種差距還會隨著項數增加而變得更大。不過我在前一段時間已經注意到了，有必要給“和”這個詞賦予一個更加廣泛的意義……。

歐拉曾幾次提議將“和”這個詞廣義化。在1 − 2 + 3 − 4 + …,的情況下，他的構想與現在所知的阿貝耳求和相似：

……毫無疑問，級數1 − 2 + 3 − 4 + 5 + …的和為⁄₄；由於它是由公式⁄₍₁₊₁₎展開而成，而此公式的值明顯為⁄₄。在考慮一般級數1 − 2x + 3x − 4x + 5x− 6x + …後這個概念變得更明晰了。這個一般級數是由表達式⁄_(1+x)展開而成，當我們讓 x = 1 後，這個級數就確確實實地相等了。

在當絕對值 |x| ＜ 1 時，有許多方式去驗證歐拉的下列等式正確：

可以將泰勒展開式的右邊拿掉，或使用正規的多項式長除。從左方開始，可採用上文的一般啟發式並嘗試乘以兩次(1+x)，或對幾何級數1 − x + x − …求平方。歐拉似乎也提出可以對後者級數的每項求微分。

以現代的眼光看，級數 1 − 2x + 3x − 4x + … 並沒有定義一個在x = 1時的函式，因此其值不能簡單地被替換為結果表達式。由於函式被定義為滿足所有的|x| ＜ 1，所以仍可取得x趨近於1的極限，而這就是阿貝耳和的定義：

歐拉與波萊爾

⁄₂−⁄₄的歐拉求和

歐拉對該級數還使用了另外一種技巧：歐拉變換，這是他自己的發明。要計算歐拉變換，首先要有可形成交錯級數的正項序列——在此情況下為1, 2, 3, 4, …。將此序列中的首項標示為 a₀。

下一步需要1, 2, 3, 4, …的前向差分；這恰好是1, 1, 1, 1, …。將該序列的首項標示為 Δa₀。歐拉變換也基於差分的差分，以及更高的疊函式，但是1, 1, 1, 1, …的前向差分為0。1 − 2 + 3 − 4 + …的歐拉變換便可定義為：

用現代術語來說，1 − 2 + 3 − 4 + …是歐拉可求和並為⁄₄。

歐拉可求和也包含有另一種可求和法。將1 − 2 + 3 − 4 + …表示為：

就有了相關的處處收斂級數：

因此 1 − 2 + 3 − 4 + … 的波萊爾和為：

比例分離

賽切夫與Woyczyński只通過兩個物理原理便得出了1 − 2 + 3 − 4 + … =⁄₄，這兩個原理分別是：無窮小鬆弛（infinitesimal relaxation）與比例分離（separation of scales）。為了表示得精確，他們為這些原理定義了一系列的“φ-求和法”，所有這些方法都可以將級數求和得⁄₄：

1 ? 2 + 3 ? 4 + …

• 如果φ(x)是一個函式，其一、二階導數在(0, ∞)上是連續可積分的，這樣的話φ(0) = 1 ，並且φ(x)的極限與xφ(x)在+∞時的值均為0，然後：

該結果推廣了阿貝耳求和，當取φ(x) = exp(−x)時可得到先前的等式。此一般陳述可通過將關於m的級數中的項配對，並將表達式變換為黎曼積分的形式予以證明。在後一步中，對1 − 1 + 1 − 1 + …的相應證明運用了中值定理，但在這裡需要泰勒公式中更強的拉格朗日形式。

廣義化

1755年的《Institutiones》上，歐拉對相似的級數求和

1 − 1 + 1 − 1 + …的三倍柯西乘積為1 − 3 + 6 − 10 + …，為三角形數的交錯級數；其阿貝耳與歐拉和為⁄₈。1 − 1 + 1 − 1 + …的四倍柯西乘積為1 − 4 + 10 − 20 + …，為四面體數的交錯級數，這個的阿貝耳和為⁄₁₆。

另一個1 − 2 + 3 − 4 + …在略微不同的方向的廣義化是級數1 − 2 + 3 − 4 + …，使用了另外的值n。對正整數n來說，此級數有下列的阿貝耳和：

其中B_n是伯努利數。對偶數n，則變為：

後一個和在1826年成為尼爾斯·亨利克·阿貝爾特別嘲笑的對象：

• “發散級數純粹是魔鬼的工作，膽敢去找到任何證明它們的行為都是羞恥的。如果用到它們，可以從中獲得想要的東西；同時也是它們，製造了如此多的不愉快與如此多的悖論。試問能想到比下面內容更令人驚恐的東西嗎：
• 0 = 1 − 2 + 3 − 4 + etc.

其中，n為正數。這是一個笑料，朋友。”

切薩羅的老師歐仁·查理·卡塔蘭也輕視發散級數。在卡塔蘭的影響下，切薩羅早期提出1 − 2 + 3 − 4 + …的“習用式”是“荒謬的等式”；而在1883年，切薩羅表明了當時的一個典型看法：公式是錯的，不過在某些場合在形式上是有用的。最後，在他1890年的書《Sur la multiplication des séries》中，切薩羅使用了一個接近於定義的模型。

此級數亦研究過n為非線性值的情況；這產生了狄利克雷η函式。歐拉研究1 − 2 + 3 − 4 + …相關級數的部分動機是η函式的泛函方程，這直接導向了黎曼ζ函式的泛函方程。歐拉在正偶整數（包括在巴塞爾問題中）時找到這些函式值的建樹已讓他聞名世界，他也試圖找到正奇整數（包括在阿培里常數中）時的值，但這個問題直到今天都是令人困惑的。η函式通過歐拉的方法解決會更加簡單，因為它的狄利克雷級數是處處阿貝耳可求和；η函式的狄利克雷級數非常難以對發散的部分求和。例如，1 − 2 + 3 − 4 + …在η函式中的相似級數是非交錯級數1 + 2 + 3 + 4 + …，該級數在現代物理學上有很深的套用，不過需要非常強的方法才能求和。